「滑らか」って何だ!? ――曲線と曲面のお話:3次元って、面白っ! 〜操さんの3次元CAD考〜(42)(5/5 ページ)
ゼブラシェーディング
ゼブラシェーディングでは、面の曲率を確認できます。ゼブラの線が途切れて隣り合う面とずれている場合には、位置だけが連続している状態、すなわち0であることが分かりますし、ゼブラの縞の線がつながってはいるが、折れ曲がっているのであればG1連続、滑らかにつながっていればG2連続であることが分かります(図16、17、18)。
また、図17のように似たような形状であったとしても、ゼブラでハイライトを掛けるとよく分かりますし、環境を映り込ませれば、G2で比較的滑らかに変わっているものが、G1などではかなり明確に不連続さが分かる場合があります。時々、似たような形状なのにスムーズさを感じたり感じなかったりするのは、「私たちの目や感覚がこの違いをとらえているから」ということが言えるのではないでしょうか。
CADにもよりますが、スケッチでは端点にG2連続による拘束条件が付けられます。それによって、制御点の動きが制限できるので、条件を崩さずに曲率をコントロールできることがあります(図19)。
また、制御点の位置は変えずに、制御点におけるウェイトを変更することで、やはり曲率の制御をすることが可能な場合もあります(図20、21)。
ということで、今回はこれくらいにしておこうと思います。
「滑らか」と一口で言ってもいろいろとあるだけです。そして、CADにもよりますが、その滑らか度合いを確認したり、あるレベルで制御することも可能だったりします。ただ、やたらと高い連続性を作り込んでも、それが必ずしも有益とはいえません。作り込みの手間やデータの重さにも効いてきます。意匠面だからG2連続まで気を使う場合がある一方で、例えば機械内部の部品は、その形状で機能することが大事であって、特に気を使わないということもあります。
要するに、「何事もそのレベルに応じた適切さが大事」ということです。
今回はこちらで失礼いたします。ではでは。
コンテンツ制作協力:Osamu Suzuki
- デスクトップ3Dプリンタ「Form2」を設計業務で使う
- クラウドCAEで静解析してみよう
- 2015年度末! 水野的 3Dデータ関連動向まとめ
- クラウド3D CAD「Onshape」と「Fusion360」で2次元図面作成機能を試す
- 無償3D CGソフト「Blender」で色付きの3Dデータを作ってカラープリントする
- 無償3D CGソフト「Blender」の操作 超基本
- 自分が使っているCADをあらためて見直してみる
- 3Dプリンタでマイミニ四駆を作る、親子教室
- STLデータを安全かつ高品質で流通させる方法
- 「滑らか」って何だ!? ――曲線と曲面のお話
- お手軽3次元CAD「MoI 3D」の新版を試してみた
- ネコ好きなシンクタンク研究員さん、モノづくりにはまる
- STLの扱いが、なんか“軽い”んだよね
- 「瞬撮」でフィギュア作ってみる? ――3Dスキャナでは考えられない早さの秘密
- 3Dモデリングの教育はどうやったら進むのか!?
- DLしたSTLデータが無償3次元CADで形状編集できない! どうしたら?
- あの無償3DCADのその後 Part2――もう少し便利に
- 無償電気CADでLEDを点灯させてみよう! ついでに筐体のSTLも
- そのSTL、ちゃんと3Dプリントできる? ――「netfabb」による簡単なSTL修正
- タダって思ったよりも高い!? 無償&廉価3Dツールとの付き合い方
- 無償3次元CADだと物足りない人に「MoI 3D」
- 3DプリンタやCADの2013年ってどうだった?
- 3DキャラのPVが簡単に作れる「キャラミん」で、3次元データ普及なるか?
- 3Dプリンタが壊れました
- レンタルのメカCADってどう思いますか?
- 夏休みの自由研究課題を3Dプリンタで作ろう
- 3Dプリンタの出力サービス、あなたは使ったことある?
- 3次元データを直接保護してくれる法律ってないのね?
- 騒いで終わりじゃもったいない。3Dプリンタブームの今後
- 設計者CAEもクラウドも「まだこれから」。2013年のCAD/CAE/PLM
- 【2013年版】3次元プリンタの普及のための5ポイント
- あの無償3DCADのその後 ――もっとCAD初心者寄りに
- CTスキャンした大腿骨のモデルに解析メッシュを切る
- CAE用ビュワーの存在とコラボレーションの必要性
- クラウド上のCAEソフトを使ってみた
- モデルをストレスなくグールグル――3次元マウス
- 初心者オジサン、伊予鉄模型で3DCADを覚える
- ダイダイダイレクト祭! その3「SolidWorks」
- ダイダイダイレクト祭! その2「Inventor Fusion」
- ダイダイダイレクト祭! その1「Solid Edge」
- お気軽だけど侮れぬ。3Dスキャナで遊んでみた
- 「妖精眼鏡」で遊んで考える、3Dデータのビジネス
- 無償のAutodesk 123Dで伊予鉄の模型を作ろう
- 趣味の切削加工は甘くない!? iModela体験記
- 小学3年生が3次元CADでモノづくりしてみた
- 自分が遊ぶものくらい自分で作ろう――FABLAB鎌倉訪問記
- 無償3DCADを試す ――そして時代は変わる?
- 3次元データと有事の関係を再考してみた
- 3次元データ形式とツールの関係を考える
- ガレージキットの世界と異分野交流実践
関連記事
 無償3次元CADだと物足りない人に「MoI 3D」
無償3次元CADだと物足りない人に「MoI 3D」
無償3次元CADもそこそこ使えると思うけれど、もう少しモデリング機能がほしい……。そう思ったときは、「MoI 3D」がよいかもしれない。 タダって思ったよりも高い!? 無償&廉価3Dツールとの付き合い方
タダって思ったよりも高い!? 無償&廉価3Dツールとの付き合い方
専門家ではなくても手が届きやすいデジタルツールである、無償3次元CADや個人向け3Dプリンタだが、やはり「無償」や「廉価」であるのには理由がある。次々と起こる問題を自力で解決できないと、使いこなせないかも。 あの無償3DCADのその後 ――もっとCAD初心者寄りに
あの無償3DCADのその後 ――もっとCAD初心者寄りに
無償3次元CAD「Autodesk 123D」の新版「Autodesk123D Design」が出た。CAD初心者にとってはすごく使いやすそう。しかし、CADに慣れた人は、もともとの123Dの方がいいかもしれない? 今回はMac版もある。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
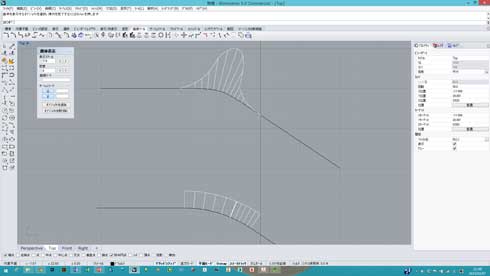 図16:曲線の曲率を確認 上がG2連続で直線から連続的に曲率が変化、下がフィレットをかけた部分で直線から非連続的に曲率が変わり、直線に戻るまで曲率が一定
図16:曲線の曲率を確認 上がG2連続で直線から連続的に曲率が変化、下がフィレットをかけた部分で直線から非連続的に曲率が変わり、直線に戻るまで曲率が一定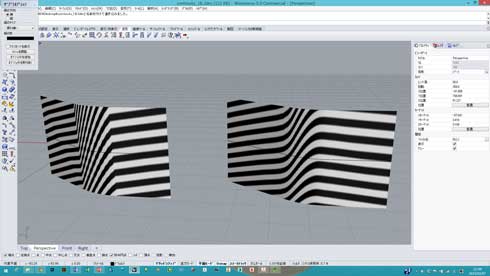 図17:図16の曲線を押し出して作った面 左のG1のものと右のG2とのゼブラの違いが分かる
図17:図16の曲線を押し出して作った面 左のG1のものと右のG2とのゼブラの違いが分かる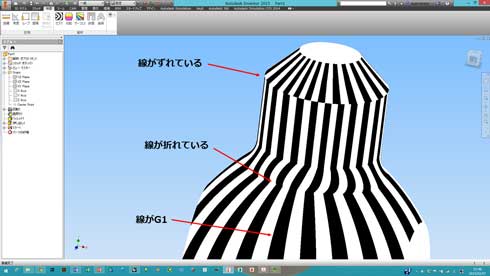 図18:曲面の連続性を見る
図18:曲面の連続性を見る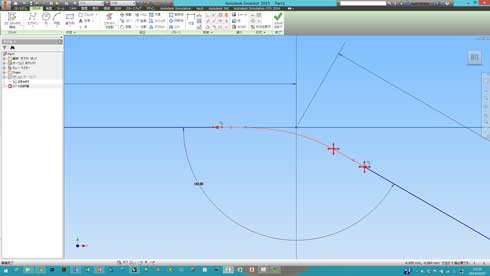 図19:このケースでは両端の直線との間にG2連続の拘束を定義しているので、それを壊すような制御点の操作ができない
図19:このケースでは両端の直線との間にG2連続の拘束を定義しているので、それを壊すような制御点の操作ができない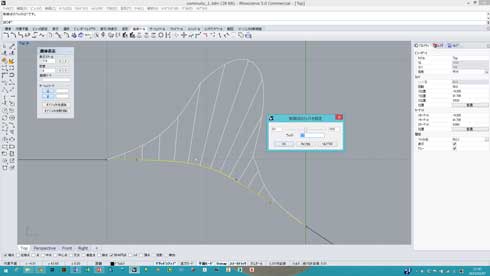 図20:黄色くハイライトされた制御点のウェイトは当初は1
図20:黄色くハイライトされた制御点のウェイトは当初は1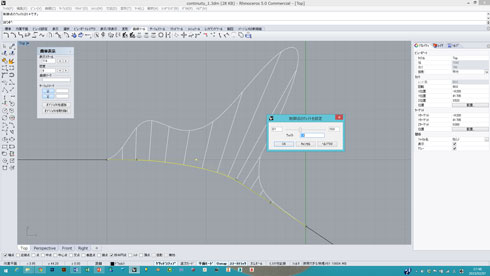 図21:制御点は動かしていないが、この点のウェイトを0.4に変更 曲率が大きく変わり、曲線自体のふくらみも変換する
図21:制御点は動かしていないが、この点のウェイトを0.4に変更 曲率が大きく変わり、曲線自体のふくらみも変換する







