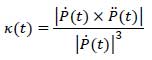「滑らか」って何だ!? ――曲線と曲面のお話:3次元って、面白っ! 〜操さんの3次元CAD考〜(42)(3/5 ページ)
接触平面とG2連続
実はさらなる連続性を考えるときには、もう1つ考えなければならない要素があります。それが「接触平面」です。
ある曲線Aを考えてみましょう。この曲線上にあるP(t0)を中心とする3つのポイントを仮定します。これらの3つの点があれば、ある平面が定義できますね。で、両脇の点を中心にあるP(t0)に果てしなく近づけていくと、どこかで極限に達するわけですが、この極限時の平面を「接触平面」と呼びます(図9)。この時、「この平面はポイントP(t0)において、最もフィットする平面」ということになるわけです。
ここに示したような、「ある平面上にある曲線」は、ある意味で特殊な曲線ですが、さらに一般的な曲線ではどうでしょうか。その場合でも、同じように接触平面を考えていくことが可能です(図10)。
先ほどのG1の条件が満たされた上で、その端点においてまず曲率が一致し、さらにその端点での接触平面も一致しているときに、「G2連続」という条件が成立します。
ねじれ率とは
3次元モデリングにおいては、大体このG2連続までくらいしか考慮していきません。実際、特に静的な状態の場合、人間の目で区別が付くのは、G2連続くらいまでといわれます。でも場合によってはさらに連続性を考えていく場合があります。
というわけで、次に登場する滑らかさのキーワードが「ねじれ率」です。また、曲線Aに登場してもらいましょう。
この曲線A上でP(s0)とP(s0+Δs)における接触平面を考えます。この2つの接触平面間の角度をΔφとし、Δsを限りなく0に近づけた極限状態を考えます。この時の極限値の値を「ねじれ率」と呼びます。ねじれ率は、「P(s0)における単位距離当たりの接触平面の変化角度で、P(s0)における接触平面の変化の割合である」といえます(図12)。
このねじれ率(τ)ですが、捩率(れいりつ)とも呼ばれ、曲線の非平面性を表すもので、完全な平面曲線の場合には0になります。ちなみに、曲率(κ)とねじれ率(τ)が共に一定な曲線であれば、3次元の螺旋(らせん)、あるいはヘリカル曲線になります。参考までに、数式でねじれ率を表現すると下記のようになります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
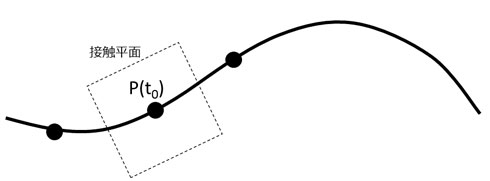 図9:接触平面
図9:接触平面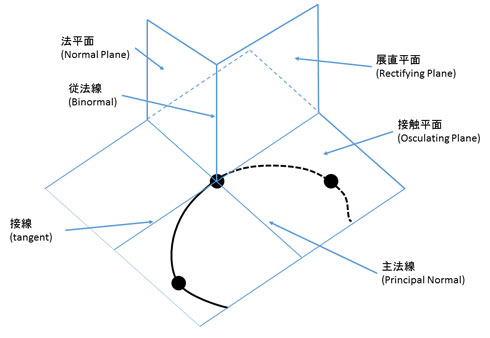 図10:一般的な曲線と接触平面
図10:一般的な曲線と接触平面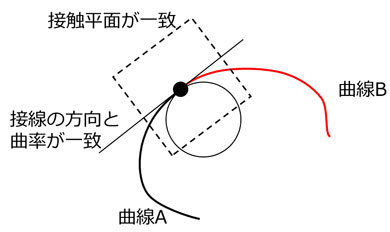 図11:G2連続
図11:G2連続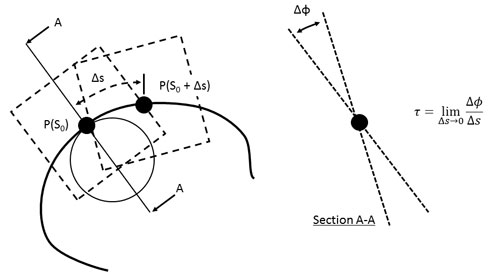 図12:ねじれ率
図12:ねじれ率