「滑らか」って何だ!? ――曲線と曲面のお話:3次元って、面白っ! 〜操さんの3次元CAD考〜(42)(4/5 ページ)
では、道路はどうして「滑らか」なのか?
難しい話はこのあたりにして、再び道路の例を考えてみましょう。先ほどの道路は滑らかなんでしょうか? 滑らかだとすると「何連続」になるのでしょうか?(図13)。
曲がっている道路を曲線に見立ててみると、曲率は連続していないと考えられます。でも、交差点のように折れ曲がっているわけではなく、その意味でスムーズには曲がっていけます。さらに、いったん直線部分を削除し、あらためてカーブの線から延長しても同じ直線道路を作れるでしょうから、接線の向きが同じということが考えられます。よって、G1連続と考えられます。
もう少し数学的に考えてみましょう。両端の真っすぐな道路は「曲線の特殊な状態」と考えると、「半径が無限大の曲線」と考えられます。ということで曲率は∞(無限大)となります。ここではハンドルは真っすぐにステイしたままです。さて、車はカーブに差し掛かります。このカーブは一定の半径の円弧と考えます。この円弧には半径があるので、その半径に沿った曲率を持っているわけです。半径は一定ですから、カーブの部分の曲率は、円弧の両端も中央部分も、ずっと一定です。つまり直線とカーブのつなぎ目で、曲率が0から突然不連続に別の値になります。また直線からモデルポイントで突如0となって、不連続になるというわけです。
ハンドルさばきとしては、一定で固定し、ハンドルを大きく切り、その後カーブにいる時は一定に切った状態で固定し、カーブを抜ける時にまた大きく切って、直線に戻れば中立状態でまた固定……という状況になります。つまり、この道路はG1連続ではなかろうかということになります。
G2レベルで滑らかにした道路は、大体こんな感じになるでしょうか(図14)。
連続性とNURBS
ところで、この連続性はCAD上では実際にどのように確認したり制御したりできるのでしょうか。それにあたって、曲線と制御点の関係を見てみましょう。
多くCADでは、曲線はNURBS(Non Uniform Rational B Spline、非一様有理Bスプライン)という曲線で表現されています。ここで、曲線と制御点の関係を見てみましょう。
制御点を使って曲線を作成していく時には、まず、端部の制御点で曲線端部の位置が特定されます。
2番目の制御点を打つ時に曲線端部の接線ベクトルが決まります。
そして、3番目の制御点を打つ時に、曲線端部の曲率が決まるということになります。
さて、そこで疑問が湧くと思います。この制御点の数では、左側の端点の接線と曲率はコントロールすることができますが、右側の端点はどうしましょう? ちょっと制御点が足りなさそうですね。このままでは左側と独立し、右側の端点は接線ベクトルも曲率も指定できません。曲線の定義の際に、制御点が多いことが良いこととは限りませんが、制御点の数が少ないと、形状表現に制限が発生してくることもまた事実です。
ところで、連続性を確認するためには、その情報を確認することが必要です。多くのプロユースのCADでは、曲率プロット(ヒゲみたいないプロット)や、面などであればゼブラシェーディングを行うことが可能です。
この手の機能が非常に豊富なものから、必要最小限のものまでさまざまですが、お手持ちのCADの機能を調べてみてください。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
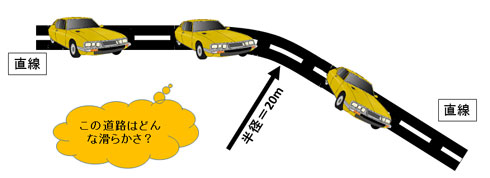 図13:道路で滑らかさを考える
図13:道路で滑らかさを考える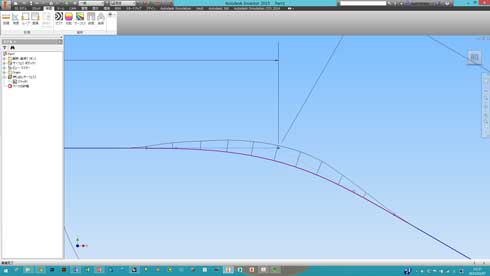 図14:G2で滑らかな道路
図14:G2で滑らかな道路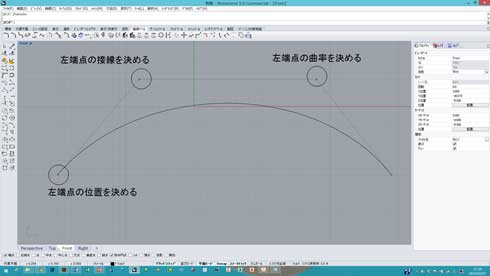 図15:制御点と曲線
図15:制御点と曲線





