クラウドCAEで静解析してみよう：3次元って、面白っ！ 〜操さんの3次元CAD考〜（50）（5/5 ページ）

[水野操 テクノロジーコラムニスト／3D-GAN，MONOist]

穴開き平板の計算

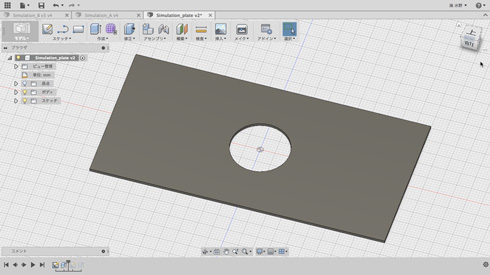
　もう1つ、計算してみましょう。これも、CAEの勉強ではおなじみの穴開き平板です。

穴開き平板

　長さ100mm、幅50mm、厚さ1mmの長方形の板に、直径が20mmの丸い穴が開いていて、そこに5000Nの荷重をかけます。

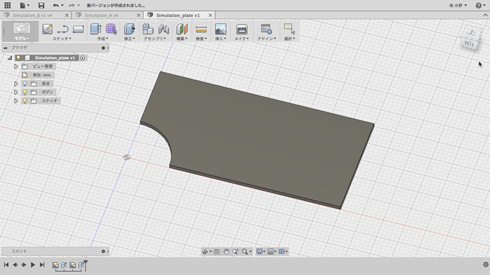
　一般に、この問題の解析では対称条件を考慮して、ジオメトリの4分の1だけ解析します。

一部分でよい

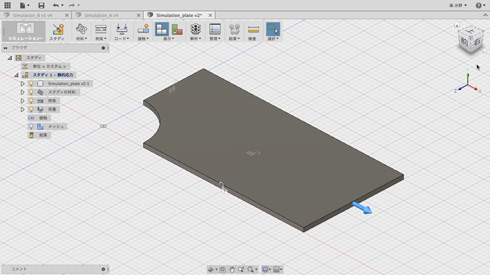
　下の面にはY方向の拘束、それぞれの対称面には対称になるようにそれぞれ、X方向の拘束とZ方向の拘束を付けます。

拘束を付ける

　で、計算しましょう。

計算した

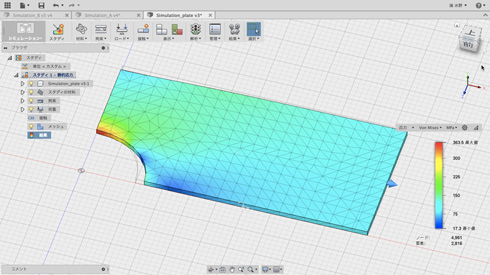
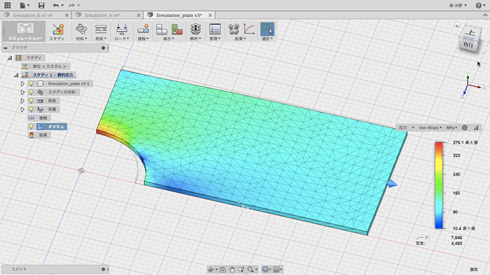
　結論から言うと、穴の上端と下端に応力集中が起きます。理論的には円孔部の平均応力に対して、3という応力集中の係数といわれていますが、実際これは板の大きさが無限であることを想定しているので、これを補正した計算式では、この集中係数は、2.25程度になります。

　今回の円孔部の平均応力は、166.7Nで、係数が2.18なので、まずまずの近い値になっていますね。

　Adaptiveで計算したら、今度は2.25になりました。

Adaptiveで計算した結果

　こちらはちゃんと計算できているようです。

適切な拘束条件、荷重条件を定義しよう

　誤解してほしくないのですが、解析結果を理論値に合わせ込むことが目的ではありません。でも、理論的（ずいぶん長い間、工学の教科書に書いてあることは、実証され正しいものであるはずなので）なことをしっかり抑えていれば、「自分が求めている結果の傾向が正しいものなのか、それとも何か違うのか」の見当がつきます。

　特に拘束条件や荷重条件は、場合によっては計算結果を激しく変えてしまうこともあるので、注意してみてください。固有値解析も、例えば、単にその形状の固有値を計算した場合と、強制変位をかけてあらかじめ応力が発生している状態では結果が違います。

　CAEでは、結局自分がどういうインプットをしたかによって、結果が違ってきますから、それ故に、今自分が与えている条件が適切なのか、自分の考えていることが適切として、そのとおりに拘束条件や荷重をかけているのかをきっちりと意識をしてみましょう。

　そこさえ押さえていれば、Fusion 360はコストパフォーマンスの高い道具だといえます。今回の記事は11インチのMacBook Air上で書きましたが、こんな小さなマシンでも、モデリングから解析まで動くのですから。

　そうはいいつつも、当然、解析はメッシュ数が多くなるほどマシンの負荷が増えますので、頻繁に本格的な解析をするのであれば、もっとパワフルなマシンで動かすことをおすすめします。解析をやる上では、マシンスペックが高すぎるということはありません。

　ということで、本日はこれにて失礼いたします。ではでは！

Profile

水野 操（みずの みさお）

1967年生まれ。ニコラデザイン・アンド・テクノロジー代表取締役。マルチ・ディメンション合同会社社長。3D-GAN理事。外資系大手PLMベンダーやコンサルティングファームにて3次元CADやCAE、エンタープライズPDMの導入に携わった他、プロダクトマーケティングやビジネスデベロップメントに従事。2004年11月にニコラデザイン・アンド・テクノロジーを起業し、オリジナルブランドの製品を展開している他、マーケティングやIT導入のコンサルティングを行っている。著書に『絵ときでわかる3次元CADの本』（日刊工業新聞社刊）などがある。

つながる、広がる、モノづくり――。「3Dモデラボ」

3Dモデルデータ投稿・共有サービス「3Dモデラボ」。3Dモデルデータを共有し、

モノづくりの楽しさをシェアしよう!!