時々刻々と変化する温度分布:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(8)(1/6 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第8回は、非定常熱伝導問題に取り組む。
今回は非定常熱伝導問題に取り組みましょう。CAE解析では「過渡熱伝導問題」となります。最後に、ちょっとしたオマケも用意しています。
その前に、サーボモーターのデザイン
まずは、連載第1回で紹介したサーボモーターのデザインの理由について触れておきます。図1はどこにでもあるサーボモーターです。ボディーはどうやらアルミダイカスト製で、黒く塗装されています。またひだひだがあるモーターも見受けられます。ひだひだは普通の誘導モーターでよく見掛けます。サーボモーターの材質と色と形状はどのような理屈で決められているか考察してみましょう。サーボモーターは定格電流よりもはるかに大きな電流を瞬間的に流すことがあるため、冷却がとても重要になります。
本連載の読者の皆さんであれば、もう理由はお分かりですよね。ボディーがアルミダイカスト製なのは、アルミニウム合金の熱伝導率が高いからです(連載第6回の表3)。ひだひだが付いているのは、熱伝達面積を大きくするためです。そして、モーターが黒く塗装されているのは、黒体放射に近づけるためでした。
熱い棒の両端に突然氷を接触させた場合
図2のような問題について考えてみましょう。100[degC]に加熱された鉄の棒があり、これを突然、両端から氷で冷やしたとします。このとき、鉄の棒は時々刻々と冷やされていきます。ここでの問題は、時間とともに変化する棒の温度を求めることが目的です。このときの条件を数式で表すと、以下のようになります(式1、式2)。
連載第2回で導出した熱伝導方程式を使います。次式です(式3、式4)。
1次元問題なので式5となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞


 式1
式1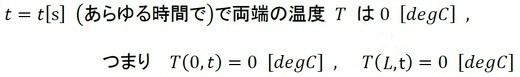 式2
式2![棒の両端の温度が突然0[degC]に固定された問題](https://image.itmedia.co.jp/mn/articles/2505/26/ay4328_coolingdesign08_fig02_w590.jpg)
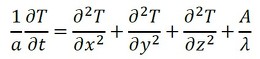 式3
式3 式4
式4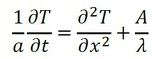 式5
式5





