基本中のキホン「熱伝導」をおさらいする:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(2)(1/4 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第2回では、基本中のキホンとなる「熱伝導」についておさらいする。
いよいよ“CAE伝熱解析”と“紙と鉛筆”による伝熱解析の説明です。
まずは、皆さん既に知っている内容だと思いますので、おさらいとなります。基本的な用語を統一したいのであらためて解説します。
熱伝導と熱伝達:1次元問題
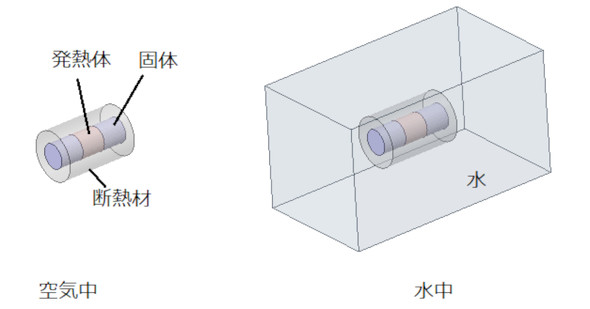
図1のような状態で、発熱体、固体、断熱材があるとします。
図1左側は空気中にある状態、図1右側は水中にある状態です。断熱材は熱を一切通さないものとします。発熱体の熱は固体を通り、固体端面の空気か水と接する面で、空気か水に伝わります。本連載の後半でダクトの熱設計を取り上げますが、ダクトに巻き付ける断熱材は若干の熱を通すので、そことは分けて考えてください。
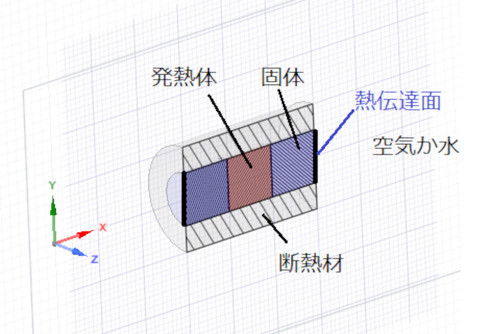
図2に、発熱体、固体、断熱材の断面図を示します。固体が空気か水に接している面を「熱伝達面」と呼ぶことにしましょう。この面は「伝熱界面」と呼ばれることもあります。そして、空気や水のことをこれからは「流体」と呼びましょう。
発熱体の熱は、固体を通過して流体に伝わります。発熱体が発する熱量(ワット数)と流体の流れの状態を与えて、発熱体内部の各点の温度と固体内部の各点の温度を求める計算が伝熱解析であり、CAE解析では熱解析と熱流体解析に対応します。後に「ふく射」の話もしますが、図2の問題を解くことが、伝熱解析のほぼ全てとなります。また、逆問題として、発熱体内の最高温度を例えば100℃にするために、水の流れの状態を求めることも伝熱解析となります。
図2を基に、発熱体と固体の温度分布を考えます。発熱体の温度が高く、固体が流体に接する面の温度が低くなると推測されます。よって、温度は座標の関数として表すことができる……というか、この関数を求めることが目的です。関数は次式で表されます。
話を簡単にするために、ここでは、温度はどのようなy座標やz座標でも“等しい”とし、x座標だけの関数とします。関数は次式で表されることになります。これを「1次元問題」といいます。
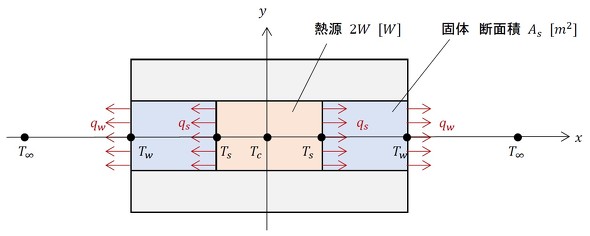
図3は、図2の断面図を正面から見たものです。各点の温度と熱流束を記入しました。
Tcは発熱体中央の温度で、この場合は最高温度となります。TsとTwは固体の両端の温度です。Twは伝熱界面の温度でもあり、添字のwは“wall”のwです。T∞は「主流の温度」と呼びます。離れた位置の流体温度だとお考えください。ただし、パイプの場合は例外で、パイプ中心の温度ではなく、水を流して冷却する場合は「混合平均温度」と呼ばれる量が使われます。
ここで、大切な量である熱流束を説明します。記号はqです。単位面積(例えば、1[m2]です)を通過する熱量で、単位は[W/m2]となります。図3の熱流束を求めましょう。熱源の発生熱量を2W[W]とすると、図3は左右対称なので、右方向に流れる熱量はその半分のW[W]です。固体の断面積をAs[m2]とすると、熱流束は式5で表されます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 製造業“現場あるある”かるた<あ行:結果発表> 秀逸作品ぞろいで審査難航!?
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 【レベル9】アセンブリ図面を作成せよ!
- 3Dプリンタ製の型を活用した、回せるネジ型チョコレートの取り扱いを開始
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 【調査レポート】設計・解析業務におけるAI活用の現実と課題
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 幾何公差の基準「データム」を理解しよう

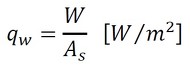 式5
式5





