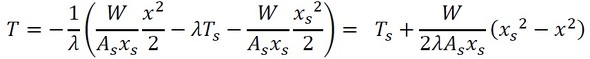基本中のキホン「熱伝導」をおさらいする:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(2)(3/4 ページ)
発熱体内部の温度分布
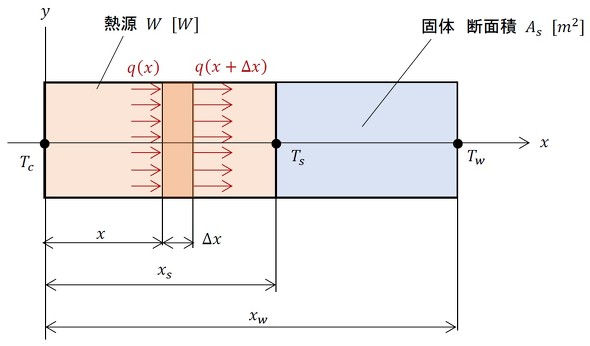
発熱体内部の温度分布を求めましょう。図3の右半分を図5に示します。幅Δxの領域の熱収支を考えます。
熱源の体積は、次の式16で表されますね。
熱源の単位体積当たりの発生熱量Aは、式17となります。
図5の幅Δxの領域の左側から入ってくる全熱量にΔxの領域で発生する熱量を足したものと、右側から出ていく全熱量が等しいと、熱収支は合っていることになります。よって、式18が成立します。
q(x+Δx)の近似値をテイラー展開を使って求めましょう。関数f(x)がaを含む区間でず〜っと微分可能であるとき、式19のように展開できます。
ここでaをxに書き換え、b−aをΔxとすると、式20が出来上ります。
式20を式19に代入します。
図5において、Δxを非常に小さい長さとすると、Δxの2乗以上の項はΔxに比べて無視できるほど小さくなるため、式21右辺の第3項以降は無視することにします。関数f(x)を関数q(x)に書き換えると、q(x+Δx)の近似値は式22となります。
式22は、以前の連載「CAEと計測技術を使った振動・騒音対策」の連載第2回で紹介しました。図にすると図6のようになり、直感的に式22が出てきます。式22の形は今後も頻出するので、頭にたたき込んでいただけると幸いです。
式22を式18に代入して、式を変形していきます。
変数分離形になったので、両辺をxで積分します。
積分定数Cを求めます。発熱体の全発熱量はWなので、x=xsの位置の熱流束は以下でした(式25)。
式24にx=xsを代入し、式24と式25が等しいので、以下のように積分定数Cが求まりました。
そして、式26と式17を式24に代入します。
あっけない式になりましたが、x=0は左右対称なものの中央なので、熱流束はゼロのはずですし、x=xsでの熱流束は式25の通りとなりました。
では、温度分布を求めましょう。フーリエの法則(式8)に式27を代入します。
変数分離形になったので、両辺をxで積分します。
積分定数Dを求めます。x=xsでT=Tsの条件を使います。
式30を式29に代入して変形します。
温度分布が求まりました。2次式(放物線)となりました。図4のような感じですね。
伝熱界面温度Tsは、式15にx=xsを代入すると求まります。最高温度Tcは、式31にx=0を代入すると求まります。流体温度と伝熱界面温度の関係は熱伝達のところで解説します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

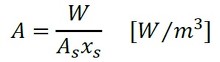 式17
式17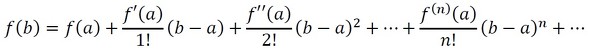
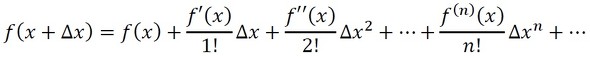
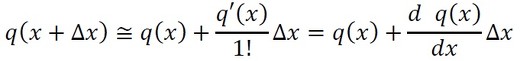 式22
式22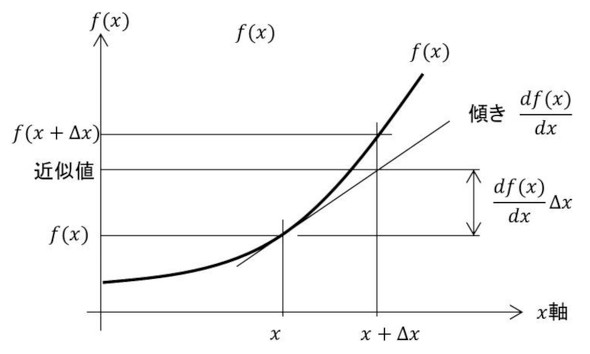
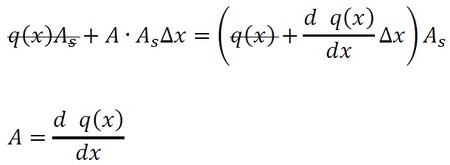 式23
式23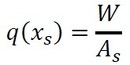 式25
式25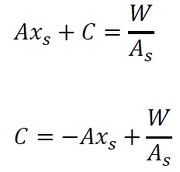 式26
式26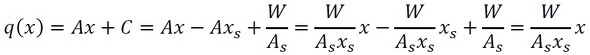
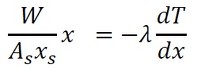 式28
式28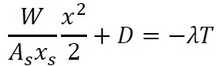 式29
式29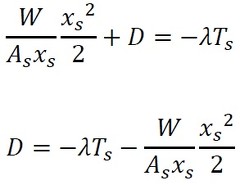 式30
式30