振動と音に関する基礎量 その1:CAEと計測技術を使った振動・騒音対策(2)(2/4 ページ)
音
音は“空気の縦振動による圧力変動”です。圧力には「ゲージ圧」と「絶対圧」がありますが、ゲージ圧の方です。単位はパスカル[Pa]となります(参考文献[1])。極端なことをいえば、マイクロフォンではなく圧力センサーで測定してもいいのです。ゲージ圧は次式で定義されます。
音が伝わる様子を図4に示します。これは「平面音波」と呼ばれるものです。まず、音源である壁が振動変位します。図4の赤色は圧力の高い領域で“プラスの圧力”です。図4の青色は圧力の低い領域で“マイナスの圧力”です。圧力の高い領域と圧力の低い領域が音速で移動します。
騒音対策に音速はあまり関係しませんが、一応書いておきますと次式となります。
参考文献:
- [1]小橋豊|基礎物理学選書4 音と音波|裳華房(S62)
音源の振動と音圧の関係
騒音対策として“音源の振動を下げる”ことがありますが、音源の振動と音圧の大切な関係を述べます。数式が出てきますが少しお付き合いください。
平面音波で説明するので、全ての量は座標xと時間tの関数です。全てのy座標、全てのz座標に対して全ての量は同じ値とします。空気の中に、辺の長さがΔx、Δy、Δzの直方体の空気に注目します。音が進行することによって、この直方体がξ(x)だけ移動し、辺Δxが少し伸びたとします。この様子を図5に示します。
変形後の辺Δxの長さは次式で表されます。
くどいようですが、微分したものを使った近似を説明しておきます。図6において、f(x+Δx)を求めたいときはその微分、つまり傾きにΔxを掛けてそれを足せば近似値が求まります。次式です。式8はこの近似を使っています。
変形前後の体積変化率aは、次式となります。
式10に式8を代入します。式9は近似式なのですが、「2次以上微小項は無視する」との表現はよく見掛けます。「近似式を使って作った微分方程式を解いても正確な答えが出るのか」との問いに答える数学力を持ち合わせておりませんので、ここでは「こそっと等号記号を『=』に書き換えておきます」といっておきます。
この直方体の運動方程式を作りましょう。f=mαの式です。直方体の質量は、密度×体積なのでρΔxΔyΔzで、速度をuとすると加速度はそれを時間で微分したものになります。直方体の左側面にp(x)の圧力が作用し、右側面にp(x+Δx)の圧力が作用しているとします。図7のような状態です。
運動方程式は次式となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

 式6
式6 式7
式7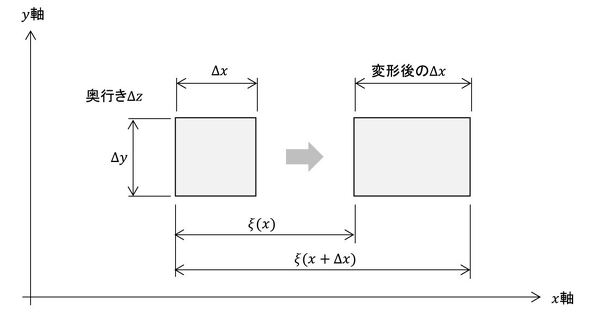
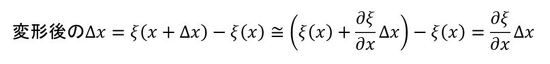 式8
式8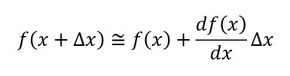 式9
式9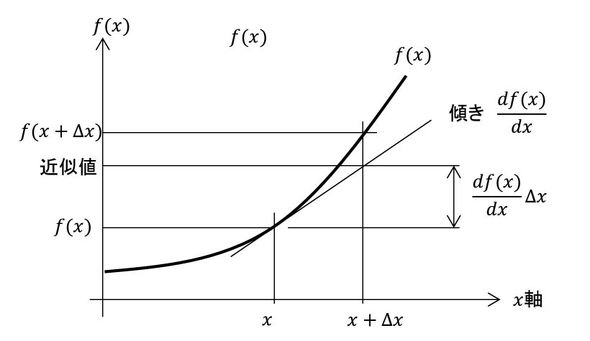
 式10
式10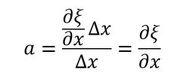 式11
式11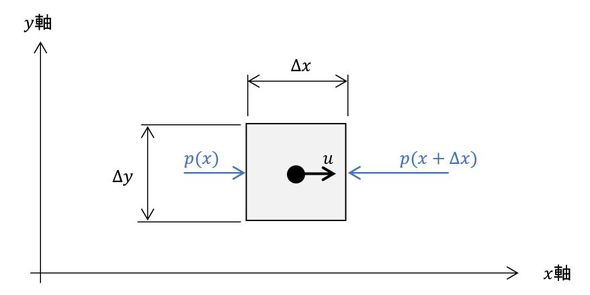
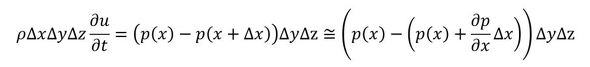 式12
式12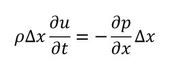 式13
式13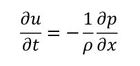 式14
式14





