振動と音に関する基礎量 その1:CAEと計測技術を使った振動・騒音対策(2)(3/4 ページ)
体積圧縮率Kという定数を導入します。例えば、100[kPa]の圧力上昇で体積が半分になったとします。体積圧縮率は次式となります。
式10で体積変化率aを求めていました。圧力とaの関係は体積圧縮率Kを用いて次式となります。
式11を代入します。
上式を時間tで微分します。
上式をもう一度時間tで微分し、式14を代入します。
式19は、1次元の波動方程式です。時間tを2階微分と座標xの2階微分が等しい関数はsinとcosでした。幾つもの波長を持つsinとcosの和が式19の解となり得ます。フーリエ級数を使って解くタイプの微分方程式ですね。今、定数cを次式で定義します。後で説明しますが、cは音速となります。
式19の解の1つとして次式が解となり得るか調べてみましょう。
式21を式19左辺に代入したものを以下に示します。分母の(t−x/c)2は2乗ではなく(t−x/c)で2回微分するという意味です。
式22を式19右辺に代入したものを以下に記します。
式22と式23は一致したので、式21は波動方程式の解の1つです。では、t=0[s]、x=0[m]の圧力値と、t=1[s]、x=c[m]の圧力値を比較すると以下となって一致します。つまり、1[s]後のc[m]離れた位置の圧力は0[s]の圧力と等しいのです。圧力が速度cで伝搬したといえます。よって、cは音速となります。
式21は音速cの進行波だと分かりましたので、微小直方体の変位ξも音速cで伝搬するはずです。よって、変位ξは次式で表されます。
変位ξを時間tで微分したものが微小直方体の速度でした。次式となります。
式17に式26を代入します。次式となります。
式20を使うと上式は次式となります。
音速cと密度ρは温度によって変化しますが、空気特有の定数です。ということは、微小直方体の速度と圧力、つまり音圧は比例関係にあります。これは重要な関係です。
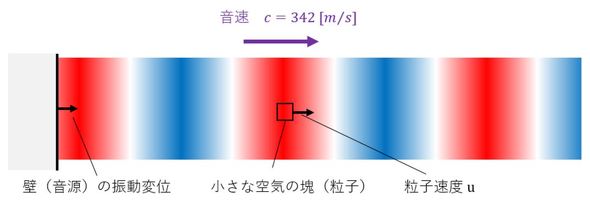
移動するのは圧力なのですが、空気の微小直方体は前述したように運動しています。そのイメージを図8に示します。
微小六面体を小さな空気の塊と考えましょう。この小さな空気の塊を「粒子」あるいは「流体粒子」と呼び、その速度を「粒子速度」といいます。粒子の運動の振動数が音の周波数となります。粒子速度と音速は関係はありますが、異なる値を持ちます。音源である壁近傍の連続性から、壁の速度と空気の粒子速度とは一致します。つまり、音圧は音源の振動速度に比例する量です。言いたかったのは以下です。
騒音対策では音源の振動速度を測定し、振動速度を低減する必要がある
なお、粒子速度は、次回紹介する「音響インテンシティ」の解説でも登場します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

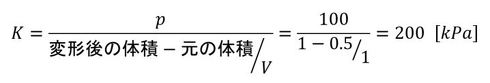 式15
式15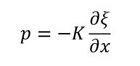 式17
式17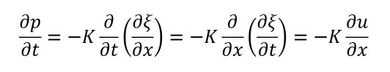 式18
式18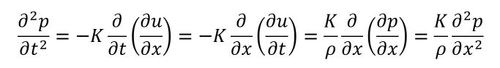 式19
式19 式20
式20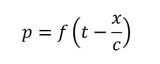 式21
式21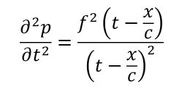 式22
式22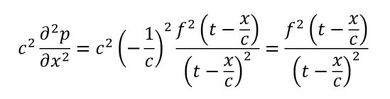 式23
式23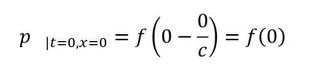 式24
式24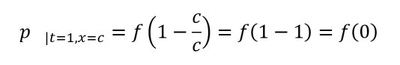 式25
式25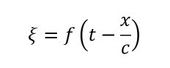 式26
式26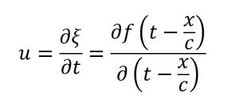 式27
式27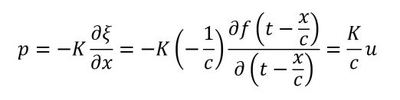 式28
式28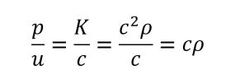 式29
式29