基本中のキホン「熱伝導」をおさらいする:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(2)(2/4 ページ)
フーリエの法則
次に、熱伝導の法則である「フーリエの法則(Fourier's law)」を説明します。図3は左右対称なので、これからは右半分だけを考えます。図4に右側の固体と固体内部の温度分布を示します。
このとき、固体内部の小さな平面を考え、そこを短い時間Δt[s]の間に通過する熱量をΔQ[J]とします。小さな平面の面積をΔs[m2]、温度分布を座標xの関数T(x)とすると、これらには以下の関係があります。これがフーリエの法則です。
参考文献[1]では、式6の微分記号は偏微分記号ですが、1次元問題なので普通の微分記号としました。単位時間(1[s]です)に通過する熱量は、ΔQをΔtで割ったもので、また、単位面積、単位時間当たりに通過する熱量は、ΔQをΔsΔtで割ったもので、これが熱流束qです。式で表すと以下となります(式7)。
式7を式6に代入すると、式8となります。こちらの方が分かりやすいですね。
式8にマイナス(−)があるのは温度勾配dT/dxがマイナスのとき、−dT/dxはプラス、つまり熱流束はプラス値となります。温度勾配がマイナスということは温度が下がっていく方向で、その方向に熱が流れるということです。
フーリエの法則の3次元版は熱流束qがベクトル量となり、次式のように表すことができます。ベクトル量は太字で表記します。
grad Tは「スカラー場Tの勾配」を表しています。∇はハミルトン演算子でベクトル量です(参考文献[2])。以降の連載の中で、∇2と表記した演算子が登場しますが、これは2つの∇同士の内積です。
参考文献:
- [1]日本機械学会|機械工学便覧 A6 熱工学(S61)
- [2]矢野健太郎|解析学概論|裳華房(S53)
固体内部の温度分布
では、固体内部の温度分布を求めましょう。固体の断面積Asは一定値なので、左側の流入熱流束qsと右側の流出熱流束qwは等しく、熱流束qをxの関数としたくても関数ではなく一定値となり、式5でした。では、式8を変形して積分しましょう。
積分定数Cは、境界条件(x=xwでT=Tw)から求めます。この条件を式12に代入すると、積分定数Cが求まります。以下です。
式14を式12に代入します。ついでに、式5も代入します。
Twは未知数なのですが、いずれ熱伝達を説明する際に流体温度から求まります。式15はxの1次式ですね。そういうわけで、図4の温度分布を直線状にしました。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞


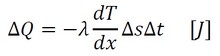 式6
式6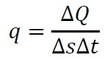 式7
式7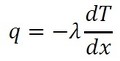 式8
式8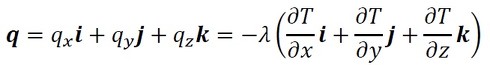 式9
式9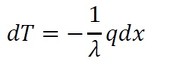 式11
式11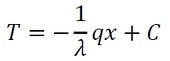 式12
式12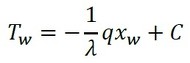 式13
式13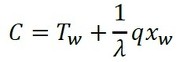 式14
式14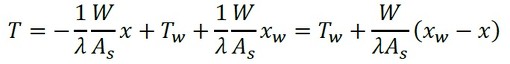 式15
式15





