公差計算の代表的な2つの考え方と使い分け：若手エンジニアのための機械設計入門（6）（1/2 ページ）

3D CADが使えるからといって、必ずしも正しい設計ができるわけではない。正しく設計するには、アナログ的な知識が不可欠だ。連載「若手エンジニアのための機械設計入門」では入門者が押さえておくべき基礎知識を解説する。第6回は、公差計算の代表的な2つの考え方と、その使い分けについて取り上げる。

[土橋美博／スワニー，MONOist]

　連載「若手エンジニアのための機械設計入門」では、機械設計を始めて間もない若手エンジニアの皆さんを対象に、機械設計で知っておくべき基礎知識や考え方などについて解説していきます。

　前回は、公差設計の必要性について取り上げました。今回は、その必要性を裏付けるもう一つの重要な理由について解説します。それは「ものにはバラつきがある」という事実です。どれだけ加工技術が進歩した現在でも、全てのものが完全に同一に仕上がることはありません。こうしたバラつきは、一般的に「4M」と呼ばれる要因によるものです。

• バラツキの要因（4M）
  • MAN（人、作業者）：習熟度によるバラつき
  • MACHINE（機械、製造設備）：機械精度やトラブルによるバラつき
  • MATERIAL（材料）：材料特性によるバラつき
  • METHOD（方法）：製造方法や製造工程によるバラつき

　この4Mがある中で、設計の狙い（設計意図）通りに製品の機能や精度を確保するには、それらのバラつきを考慮に入れた上で、あらかじめ設計上の許容範囲を決めておく必要があります。これが「公差」であり、その許容範囲をどう定めるかが「公差計算」です。ここからは、公差計算の代表的な考え方について説明します。

公差計算の基本的な考え方

　公差とは、先に紹介した4Mのように、加工において避けることができない誤差に対し、許容される数値の上限と下限との差（＝許容範囲）を示したものです。組み立て製品の品質や精度を保つためには、この公差をどのように計算するかが非常に重要になります。ここでは、公差計算の代表的な考え方である「互換性の方法」と「不完全互換性の方法」の2つについて説明します。

（1）互換性の方法（ワーストケース※1計算／Σ（シグマ）計算）

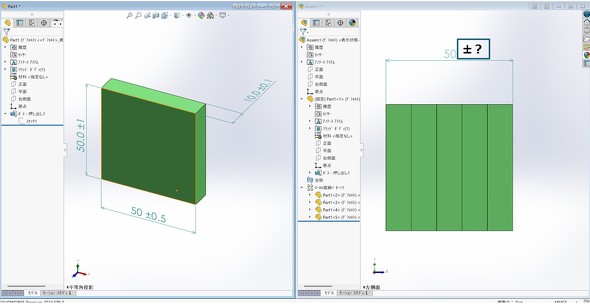
　この方法は、公差の「最大値と最小値が最も極端に組み合わさった状態」を想定して計算するものです。例えば、5つの部品で構成されるアセンブリ（組立品）を考えてみましょう。それぞれの部品に±0.1mmの公差が設定されていた場合、全ての部品が最大値または最小値に振れていたとしたら、組み立て後の全体の寸法はどのようになるでしょうか。

※1：ワーストケース：直訳すると「最悪の場合」という意味ですが、ここではあくまで許容値の範囲内で最大に寸法が振れた場合を意味します。実際に悪い結果という意味ではありません。

図1　板厚10±0.1mmの部品を5枚並べた場合の図示寸法と許容差の和（合計）［クリックで拡大］

　このとき、図示寸法の和と許容差の和は次のように計算します。

計算式

• 図示寸法の和：10＋10＋10＋10＋10＝50
• 許容差の和：±0.1＋±0.1＋±0.1＋±0.1＋±0.1＝±0.5
• 合計寸法（図示寸法／サイズ公差）：50±0.5

　この計算方法の特徴は、10±0.1mmの公差を持つ部品を用いた場合でも、この方法で算出された総厚50±0.5mmの範囲内に必ず収まるという点です。どの部品を交換しても組み立て後の全体寸法が許容範囲内に収まるため、部品を完全に互換できる、すなわち交換しても問題ないことになります。このように、部品間の互換性を前提とした設計手法であるため、互換性の方法と呼ばれています。

（2）不完全互換性の方法（統計的計算／√（ルート）計算）

　もう一つの考え方として、「全ての部品が最大値や最小値になるとは限らない」という、統計的な視点を取り入れた方法があります。実際の加工においては、公差範囲を±0.1mmに設定していたとしても、多くの部品はその端の値（±0.1mm）にはならず、中心値（例えば、10.0mm）を基準としたバラつきが生じます。このバラつきは、一般的に正規分布（平均値を中心とした山型の分布）で表現されます。

図2　正規分布のイメージ［クリックで拡大］

　図2の左側は、±σ、±2σ、±3σに対応する正規分布の例を示しています。図2の右側では、±3σの範囲内に99.7％のデータが存在し、両端の0.3％はその範囲外に位置することを表しています。つまり、「±3σで管理された部品の場合、統計的には約0.3％の部品が許容範囲（±0.1mm）を外れる」と考えることができます。これは1000個生産した場合、およそ3個が規格外となる可能性があることを意味します。

　このような統計的アプローチでは、次のような計算を行います。

計算式

• 図示寸法の和：10＋10＋10＋10＋10＝50
• 許容差の和：±√0.1²＋0.1²＋0.1²＋0.1²＋0.1²＝±√0.05≒±0.22
• 合計寸法（図示寸法／サイズ公差）：50±0.22

　このように、各部品の寸法が「±3σの正規分布内にある」と仮定した場合、統計的には99.7％の確率で、合計寸法が50±0.22mmの範囲に収まると評価できます。これはあくまで確率ベースの公差計算であり、実際にはわずかですが、規格外となる部品が含まれる可能性がある点に注意が必要です。

　この方法では、全ての部品が必ず許容範囲内に収まるとは限らないため、前述の互換性の方法とは異なり、どの部品を交換しても常に組み立て後の寸法が保証されるわけではありません。完全に互換できない（交換して問題は起こり得る）という性質から、この手法は不完全互換性の方法と呼ばれています。