1980年代のものづくり 〜大学から企業での研究開発へ〜：ものづくりをもっと良いものへ（2）（1/2 ページ）

本連載では、エンジニアとして歩んできた筆者の50年の経験を起点に、ものづくりがどのように変遷してきたのかを整理し、その背景に潜むさまざまな要因を解き明かす。同時に、ものづくりの環境やひとづくりの仕組みを考察し、“ものづくりをもっと良いものへ”とするための提言へとつなげていくことを目指す。第2回は、1980年代のものづくりを振り返る。

[大富浩一／日本機械学会 設計研究会，MONOist]

　第2回では、1980年代のものづくりについて紹介する。前回でも述べたが、本連載はこの半世紀のものづくりを網羅的に取り上げるものではなく、あくまで筆者自身の経験を通じて紹介するものである。そのため、一般的に知られる事実と若干異なる部分があるかもしれないが、その点はご容赦いただきたい。

　一方で、実際に経験した者でなければ分からない事象を通して、その背景に潜むさまざまな要因を明らかにしていく。同時に、ものづくりの環境やひとづくりの仕組みを考察し、“ものづくりをもっと良いものへ”とするための提言へつなげていくことを目指す。

　今回から数回は、年代ごとに筆者が実際に経験した出来事を通じて、読者の皆さまに知ってもらいたいことを紹介する。それ以降は、いくつかのテーマをさらに深掘りし、今後のものづくりのあるべき姿についての提言へとつなげていきたい。

注：「モノ」「もの」の表記について、本稿では「モノ：生産要素または経営資源といった手段」「もの：生産活動により付加価値を持った成果物」と使い分けて表記しています。また、「人」「ヒト」「ひと」の表記については「人：一般的」「ヒト：生物学的」「ひと：人間的（ものとの対比）」と使い分けています。

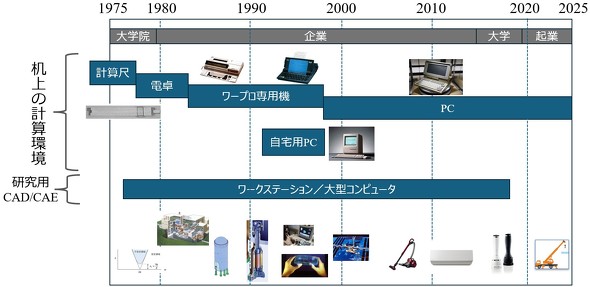
計算機の変遷

　図1に、筆者がこの50年間で使用してきた計算機の変遷を示す。

図1　筆者がこの50年間で使用してきた計算環境の変遷［クリックで拡大］

　一般的な計算機の発展については多くの文献があるため、詳細はそちらを参照いただきたい。ここでは、筆者が日常業務の中で実際に使用していた計算環境を示す。本稿では図の詳細な説明は行わず、今後の各回でこの図を用いながら解説を進めていく。

　1980年代後半には、文書作成が可能なワープロ専用機が登場し、手書きからの解放が始まった。当初は2行表示であり、間もなく「三行革命」とうたわれた3行表示の機種が登場して、ようやく実用の域に達した。40行表示機が登場したのは1990年代中期以降であり、その後、PCの普及とともに姿を消していった。

大学時代

　筆者が大学に在籍していたのは1971〜1979年なので、正確には1980年代ではないが、この時代に使われていた「計算尺」について紹介したい。計算尺は、四則演算が可能な道具であり、有効数字の概念を必要とする点で工学的センスを磨く上でも重要な存在であった。ここであらためて紹介しておきたい。

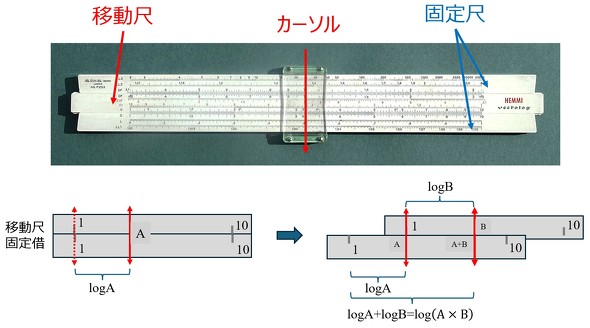
　図2上図に計算尺の外観と構造を示す。

図2　計算尺の構造と計算の原理［クリックで拡大］

　計算尺は本体（固定尺を含む）、移動尺、カーソルから構成されている（呼称は当時異なっていたかもしれない）。幅は約30cm、厚さは約1cmで、筆者が使用していたものは竹製であり、表面は写真のように白い部材でコーティングされていた。竹製が採用されていたのは、固定尺と移動尺の伸縮差を最小化するためであったと考えられる。固定尺は上下に分かれ、裏面で連結されている。移動尺は上下の固定尺に挟まれた状態で横方向にスライドできる。カーソルは本体側面の溝を介して横にスライド可能で、中央には細い指標線が引かれており、この線を用いて数値の読み取りを行う。

　図2下図に、計算尺の原理を示す。足し算や引き算は積み木と同じ原理で、2つの積み木（それぞれの高さをA、Bとする）を積み重ねたとき、その合計の高さを測るとA＋Bとなる。この原理を利用している。つまり、同じ目盛を持つ2本の線形尺を固定尺と移動尺として組み合わせればよい。これは図2上図の上半分に示した固定尺と移動尺に対応している。

　一方、掛け算や割り算の計算には、次の関係式を利用する。

log（A×B）＝logA＋logB，log（A／B）＝logA−logB

　すなわち、図2下図に示すように、対数尺を用いる。2つの同じ対数尺を固定尺と移動尺として組み合わせることで、掛け算や割り算を行うことができる。これは図2上図の下半分に示した固定尺と移動尺に対応している。使い方は足し算や引き算の場合と同じであり、異なるのは尺の目盛が対数表記になっている点である。

　計算尺は、上記のように数学の公式を応用してさまざまな計算を行うことができるが、筆者は主に四則演算で使用していた。

　実際の計算では、例えば、346.43×791.23のような計算を行う場合がある。

　このときは、3.4643×10²×7.9123×10²と分解し、目盛で読み取れる範囲（解像度）で3.4643×7.9123の計算を計算尺で行い、10⁴の処理は頭の中で行う。このように計算尺は、電卓のように多桁の演算を行うものではなく、有効数字を用いて大まかに結果を見積もる道具である。大ざっぱではあるが、桁を間違えずに全体を把握することは、ものごとを俯瞰して捉える力につながるのではないかと考える。

　筆者の大学時代と現在の大学教育を比較して感じるのは、現物教育の重要性である。筆者の学生時代は、工作実習を通じてモノのイメージをつかみながら製図を学んでいたため、特に違和感はなかった。しかし、近年、大学で製図法を教えた経験から見ると、現在の教育内容で学生が十分に理解できているとは言い難い。大学は、モノ（形状）を認識する力を養う教育にこそ注力すべきであり、それが身に付いた上での製図教育でなければ意味がない。また、大学で教えられている表記法は国際的なものとは異なっており、企業に入ってから戸惑う学生も少なくないと聞く。“図面”については、別途テーマを設けて考察したい。