基本中のキホン「熱伝導」をおさらいする:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(2)(4/4 ページ)
熱伝導方程式の導出
前項では、幅Δxの領域の熱収支について、入ってくる1秒当たりの熱と出ていく1秒当たりの熱が等しいとしました。ここで、“入ってくる熱の方が多く、発熱体が加熱される状態”を考えます。次式となります。
1秒当たりの温度上昇は、温度上昇速度と捉えることができます。式33で表しましょう。
加熱に使われる熱は、1秒当たりの温度上昇量に質量と比熱を掛けたものになります。式18を変形して、加熱に使われる熱を加えると式34となります。
式22を代入した後、式を変形していきましょう。
フーリエの法則(式8)を代入します。
定数をひとまとめにします。以下に記す温度伝導率aを次式で定義し、式36に代入します。ついでに、微分記号を偏微分記号に変更します。
さらに、3次元版に拡張しましょう。温度Tは座標(x,y,z)と時間tの関数と考えることができ、T(t,x,y,z)と表せます。
ナブラ演算子(参考文献[2])∇を使うと、式40となります。∇2は、ナブラ演算子同士の内積で「ラプラス演算子」というそうです。
参考文献[1]に載っている式が出来上りました。これが熱伝導方程式の一般形となります。温度伝導率aにも意味があって、温度の伝わりやすさと解釈できます。後は、流体の主流の温度T∞と伝熱界面の温度Twの関係が分かれば、全ての温度が求まります。これには「熱伝達率」というパラメーターを使います。次回以降は熱伝達率を説明し、ヒートシンクの熱解析をシミュレーションと、紙と鉛筆で行っていきます。 (次回へ続く)
参考文献:
- [1]日本機械学会|機械工学便覧 A6 熱工学(S61)
- [2]矢野健太郎|解析学概論|裳華房(S53)
Profile
高橋 良一(たかはし りょういち)
RTデザインラボ 代表
1961年生まれ。技術士(機械部門)、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。
構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置(MRI装置)の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在RTデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ RTデザインラボ
関連記事
 ストップ! 外注丸投げ――CAE解析や冷却系の設計を自分でやれるようになろう
ストップ! 外注丸投げ――CAE解析や冷却系の設計を自分でやれるようになろう
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第1回では、冷却系設計に関する題材をいくつか紹介し、本連載で取り上げるトピックスについて整理する。 CAEソフトに仕掛けられたトラップ
CAEソフトに仕掛けられたトラップ
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。第1回のテーマは「CAEソフトに仕掛けられたトラップ」だ。 連載「CAEを正しく使い疲労強度計算と有機的につなげる」の内容と有限要素法
連載「CAEを正しく使い疲労強度計算と有機的につなげる」の内容と有限要素法
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第2回では本連載の「あらすじ」と「有限要素法」について取り上げる。 解析専任者に連絡する前に、設計者がやるべきこと
解析専任者に連絡する前に、設計者がやるべきこと
連載「CAEと計測技術を使った振動・騒音対策」では、“解析専任者に連絡する前に、設計者がやるべきこと”を主眼に、CAEと計測技術を用いた機械の振動対策と騒音対策の考え方や、その手順について詳しく解説する。連載第1回では、本連載の趣旨、振動対策や騒音対策が必要となる場面などについて取り上げる。 設計者なら一度はやってみたい形状最適化、お金をかけずにどこまでできる?
設計者なら一度はやってみたい形状最適化、お金をかけずにどこまでできる?
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。 その設計、そのボルトと本数で大丈夫?
その設計、そのボルトと本数で大丈夫?
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。また、連載の中で、ボルト締結の基礎である締め付けトルクと軸力の関係や、締め付けトルクの決定方法などについても取り上げる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

 式33
式33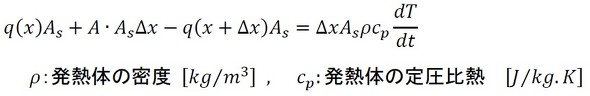
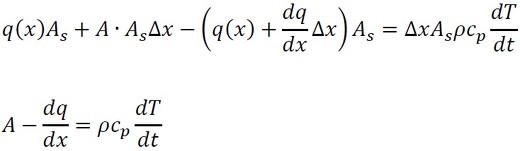 式35
式35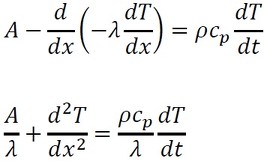 式36
式36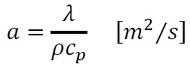 式37
式37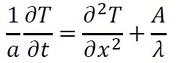 式38
式38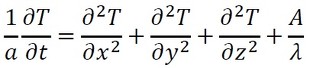 式39
式39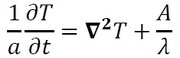 式40
式40






