CAEソフトに仕掛けられたトラップ:CAEを正しく使い疲労強度計算と有機的につなげる(1)(1/4 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。第1回のテーマは「CAEソフトに仕掛けられたトラップ」だ。
今回からお届けする新連載のテーマは、“CAEを正しく使って、解析結果から疲労破壊の有無を予測しよう!”です。「……えっ? うちの会社、CAEソフト付きの3D CADを導入してるし、そんなのもうやってるよ。それに解析専任者もいるし!」という声が聞こえます。
前回シリーズ「CAEと計測技術を使った振動・騒音対策」では、「冴えない機械の救いかた」的な内容を紹介しました。さらにその前のシリーズ「フリーFEMソフトとExcelマクロで形状最適化」では、トポロジー最適化(位相最適化)について取り上げました。「なるほど、いよいよ筆者はネタがなくなってしまい、今度は強度計算か?」という声も聞こえてきます……。取りあえず進みましょう。
応力計算が得意なはずの有限要素法
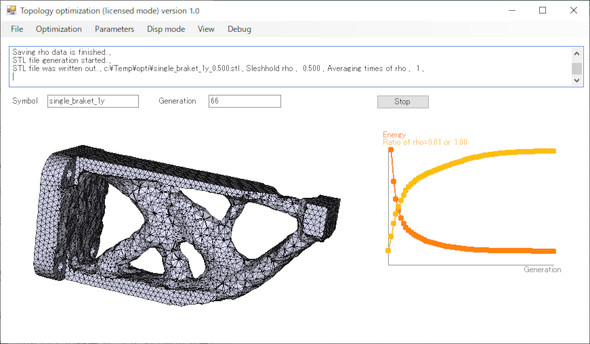
応力計算、特に応力集中部の計算が得意なはずの有限要素法です。ブラケットを題材にして強度計算のためのCAE解析をやってみましょう。題材の形状はトポロジー最適化で作りましょう。図1のような形となりました。
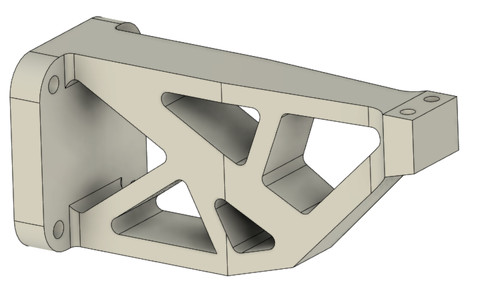
以前の連載の中で、トポロジー最適化ソフトが出力するSTL形式の3Dデータを使って金属3Dプリンタで出力したら、近い将来痛い目に合う旨の話をしましたので、鋳造で作ることにします。図2のような形状をモデリングしました。鋳物だとボルトの座面の処理が必要ですが、今回は省略しました。
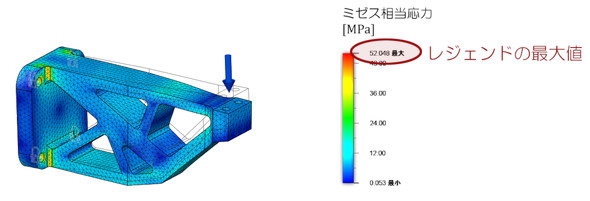
図3に単品解析結果を示します。
ここで「レジェンドの最大値」を見て、「52[MPa]、FC250材(ねずみ鋳鉄の一種)の引張強さは250[MPa]だから、安全率は5[-]だな。鋳物は脆性材料なのでもう少しマージンがほしいところだが、これでよしとしよう」と考えたあなた! シミュレーションの神様のささやきが聞こえてきませんか?
オマエ、本当にそれでいいと思っているのかい?
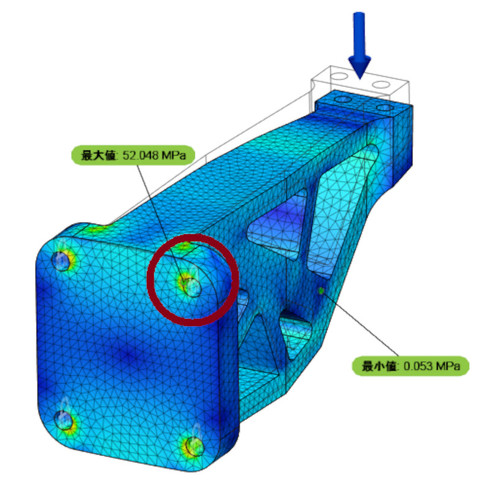
幸運にもシミュレーションの神様のささやきが聞こえたあなたは、最大応力が発生する場所を調べることにしました。図4に示すようにボルト穴のエッジでした。
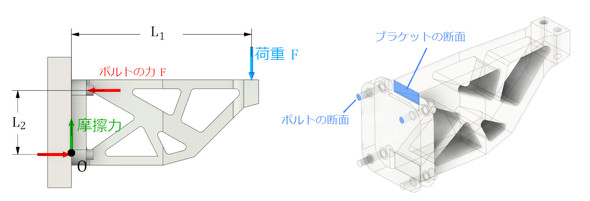
拘束境界条件をボルト穴にしていたようです。続いて、あなたは「ここが最大応力になるということは、ボルトにも荷重がかかりそうだな。ボルトにかかる力はこんな感じかな」と、図5左図のような力のつり合い図を描いてみました。
つり合い図はちょっと怪しいですが、さらに、O点周りのモーメントのつり合いを確認したあなたは、ボルトの力Fが荷重Wよりもはるかに大きいことに気付きました。そして、力Fを負担する断面を想像してみたところ、図5右図のように、ボルトの断面がブラケットの断面より圧倒的に小さいことにも気が付き、ボルトをモデリングして解析することにしました。
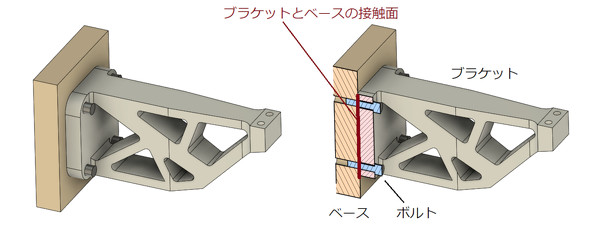
解析モデルを図6に示します。何回かの試行錯誤の末、あなたはブラケットとベースの接触面に接触要素を設置しなければボルトに応力が発生しないことに気が付きました。ブラケットとベースの接触面は摩擦係数0.15[-]の接触要素、それ以外の接触面には固着の接触要素を設置してあります。
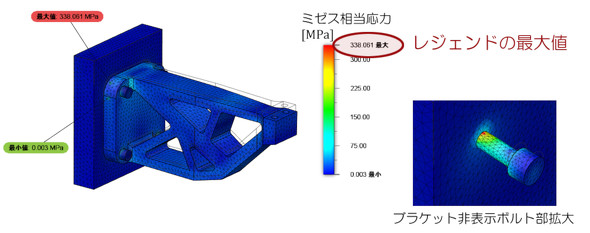
図7に解析結果を示します。
これを見て、あなたは「うげっ! 応力が6倍になってボルトに応力集中が発生している。こんなのデザインレビューで見せたらレビューは絶対パスしない。どうしよう……」と頭を抱えるのでした。
さて、いくつかツッコミどころがありますが、いったん次に行きましょう!
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞