CAEソフトに仕掛けられたトラップ:CAEを正しく使い疲労強度計算と有機的につなげる(1)(2/4 ページ)
応力計算が得意なはずの有限要素法:片持ちはり
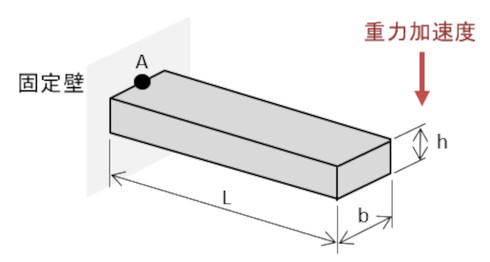
訳が分からなくなったときは、答えの分かっている問題を解いてみるのも策です。図8に示す自重が作用する片持ちはりを解いてみましょう。
条件は次式とします。
断面二次モーメント、単位長さ当たりの荷重、図8のA点の曲げモーメントは次式となります。
図8のA点の曲げ応力は次式ですね。
ではやってみましょう。境界条件を図9に、X方向応力分布を図10に示します。
A点の応力、つまり最大応力ですが1.013[MPa]となり、はり理論値から10[%]ほど大きくなりました。要素分割を細かくしたら解析精度が良くなるはずです。要素サイズを半分にした解析結果を図11に示します。
A点の応力、つまり最大応力は1.226[MPa]と、はり理論値から30[%]ほど大きくなりました。「だってこれ、フリーソフトでしょ!?」って思われたかもしれません。であれば、有名なソルバーを使いましょう。
ソフト、お借りします
ソルバーに「Nastran」を採用している3D CADはいくつかあるのでそれを使いましょう。Nastranは、航空宇宙、自動車、造船、機械、電気電子、建築、土木などの多岐にわたる分野で、数多くの研究機関や企業に広く利用され、世界のデファクトスタンダードとして高い評価を得ているはずです。では、使ってみましょう。
図12に解析結果を示します。A点の応力は1.109[MPa]です。「げっ! 理論値より20[%]も大きいじゃないか!?」との印象をお持ちの方がいるかもしれません。
20[%]も異なるのは少し腑に落ちません。原点に立ち戻って答えの分かっている問題を解いたはずですが、なぜでしょうか……。シミュレーションの神様に見捨てられた気分です。
最近使ったソフトが怪しい
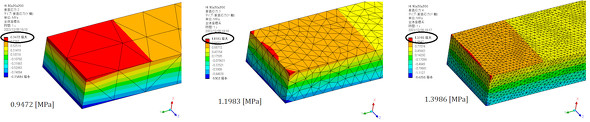
では、あと1つ有名な有限要素法ソフトである「ANSYS」でやってみましょう。要素分割を変えて計算した結果を図13に示します。最も細かい要素分割の結果は1.3986[MPa]です。「げげっ!! 今度は40[%]以上も違っているじゃん!!」という事態になりました。
要素分割を細かくすれば解析精度が良くなることには反対しませんので、ここでは最も細かい要素分割の結果を採用しましょう。40[%]以上違っているので、ソフトに「オマエ、怪し過ぎるぞ!」なんて失礼なことは言えませんね。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
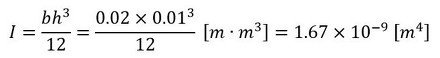 式3
式3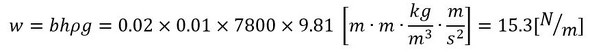 式4
式4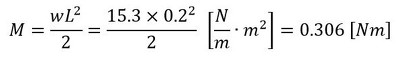 式5
式5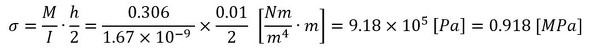 式6
式6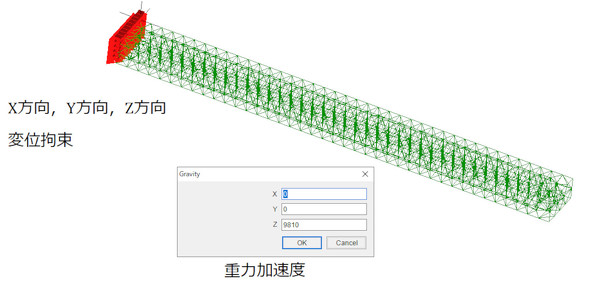
![自重が作用する片持ちはり解析結果(要素サイズ:5[mm])](https://image.itmedia.co.jp/mn/articles/2402/14/ay4328_caefatigue01_fig10_w590.jpg)
![自重が作用する片持ちはり解析結果(要素サイズ:2.5[mm])](https://image.itmedia.co.jp/mn/articles/2402/14/ay4328_caefatigue01_fig11_w590.jpg)
![自重が作用する片持ちはり解析結果 Nastran(要素サイズ:2.5[mm])](https://image.itmedia.co.jp/mn/articles/2402/14/ay4328_caefatigue01_fig12_w590.jpg)