ボルト締結体に作用できる許容繰り返し荷重:CAEを正しく使い疲労強度計算と有機的につなげる(17)(1/4 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第17回では「ボルト締結体に作用できる許容繰り返し荷重」について取り上げる。
前回までの内容から、ボルトに発生する応力振幅を求めることができるようになりました。とすると、ボルトが疲労破断しない条件を満たす繰り返し荷重も求まります。ボルトが1本の場合と複数本の場合の応力振幅と許容繰り返し荷重を比較してみましょう。
ボルトが1本の場合と複数本の場合の応力振幅と許容繰り返し荷重
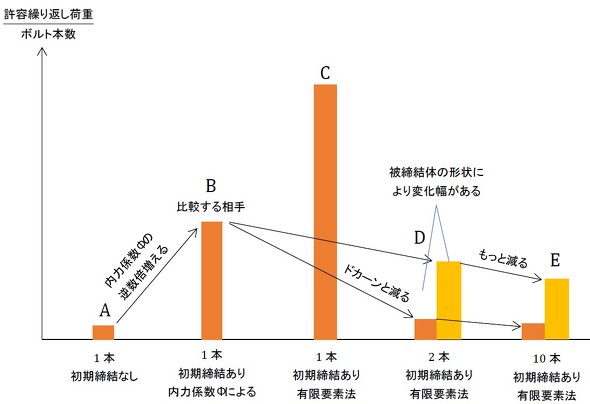
被締結体には繰り返し荷重が作用するとして、ボルトに発生する応力振幅がちょうどボルトの疲労強度(ないしは疲労強度を安全率で割った値)に等しくなるような繰り返し荷重(許容繰り返し荷重)を説明しようと思いますが、結果だけを先に述べると図1のようになります。許容繰り返し荷重と応力振幅は逆数の関係になります。
図1のAは「荷重をボルトの有効断面積で割った応力の2分の1が疲労強度に一致する荷重」です。単純に「荷重÷断面積の半分」です。図1のBは内力係数Φを考慮したものです。ねじの文献の範ちゅうでBを求めることができるので、Bの許容繰り返し荷重を比較対象のベースとします。
図1のCですが、ボルト1本の場合について有限要素法で応力振幅を求めると、内力係数を考慮した値よりもかなり小さくなります(参考文献[1])。ユンカーはこのことに気付いていて経験的な係数を掛けていたそうです。現在では数表があります。筆者の場合は有限要素法解析をしているときに気付きました。
図1のDが本題です。ボルトが2本の場合は荷重の作用線とボルトの軸が一致しなくなり、ボルトには偏心荷重が作用して曲げ応力が発生します。すると、途端に応力振幅が大きくなり、許容繰り返し荷重は「ドカーン」と小さくなります。応力振幅の大きさは被締結体の形状により変化しますが、条件が悪いと図1のAに近い値まで減少します。Aに近い値になるということは、内力係数の効果がないに等しく、少しショックです。通常のホルト締結体の設計はBの値をベースとするのですが、例えば、ボルト2本として設計した場合、許容繰り返し荷重はBの2倍ということではなく、それよりもかなり小さな値にしなければなりません。図1のEはボルト10本の場合です。2本よりもさらに小さくなります。
それでは図1のB、C、D、Eを有限要素法で求めましょう。
参考文献:
- [1]吉本他|ねじ締結体の内力係数|日本機械学会論文集|42巻359号(S51)
ボルトに発生する応力振幅と許容繰り返し荷重:ボルト1本
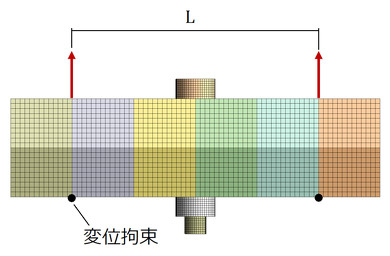
連載第14回で、内力係数Φを有限要素法で求めました。この続きとなります。図2に荷重条件と拘束条件を示します。連載第14回で述べたのはL=0[mm]の場合でした。
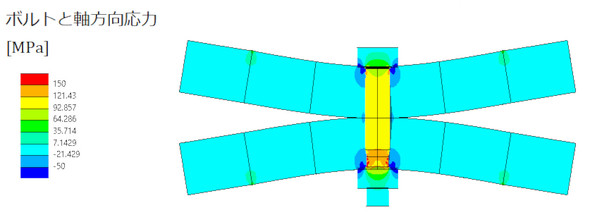
ボルトに初期締結力を与えることと、応力振幅の求め方は既に説明しました。L=0[mm]のときのシミュレーションで求めた内力係数と文献の式による内力係数がほぼ一致しました。この条件が図1のBです。L寸法を変えたときの解析結果を図3と表1に示します。L寸法によって応力振幅が変化しており、L=0[mm]のときよりもかなり小さくなっています。これらが図1のCとなります。内力係数Φに換算すると、L=0[mm]のときのΦが0.130[-]であるのに対し、L=50[mm]のときのΦは0.023[-]と約6分の1になります。
| 単位 | L=0[mm] | L=50[mm] | L=100[mm] | L=150[mm] | |
|---|---|---|---|---|---|
| 荷重 | N | 5566 | 5566 | 5566 | 5566 |
| 初期応力 | MPa | 138 | 138 | 138 | 138 |
| 荷重時応力 | MPa | 150 | 140 | 142 | 145 |
| 応力振幅 | MPa | 6.095 | 1.06 | 2.065 | 3.355 |
| 内力係数Φ | − | 0.13 | 0.023 | 0.044 | 0.072 |
| 表1 解析結果 | |||||
初期締結力がかなり小さいのですが、その理由は前回述べた締め付け係数Qを3[-]としたためです。しかし、少し小さ過ぎましたね。被締結体に掛けられる許容繰り返し荷重を求めましょう。その前に、図1のAである「荷重をボルトの有効断面積で割った応力の半分が疲労強度に一致する荷重」、つまり許容繰り返し荷重は、例えばM10の場合には式1となります。
許容繰り返し荷重は、荷重振幅の2倍ですね。
ボルトの初期締結がある場合の被締結体に掛けられる荷重(許容繰り返し荷重:締め付けあり)は式3です。
表1のΦの値から許容繰り返し荷重はかなり大きくなります。しかし、初期締結力よりも大きくできません。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

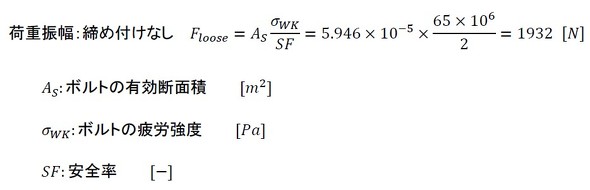 式1
式1 式3
式3





