「ねじ締結体」を理解する:CAEを正しく使い疲労強度計算と有機的につなげる(14)(1/4 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第14回では、本連載の2つ目の本丸である「ねじ締結体」について取り上げる。
本連載の2つ目の本丸、「ねじ締結体」について取り上げます。まずは、いくつかの重要なポイントをおさらいしましょう。
締め付けトルクと軸力のおさらい
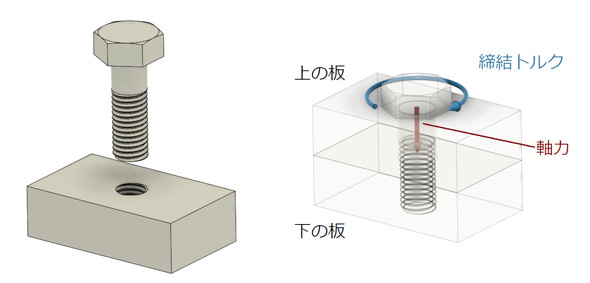
図1に締結トルクと軸力を示します。ボルトの頭を回すとボルトには軸力が発生し、ボルトの頭はその軸力で上の板を押します。同時に下の板は軸力と同じ大きさの反対方向の力で上の板を押します。
ボルト締め付けトルクと軸力(初期締結力)の関係はJIS規格の式(参考文献[1])を使えば求まります。締結トルクと軸力の関係を以下に記します(式1)。
トルク係数は次式で表されます。
式2の導出については、連載「設計者向けCAEを使ったボルト締結部の設計」の中で説明しています。ボルトの締結トルクは、ボルトの強度によって変えます。高強度ボルトの締結トルクは高い値となります。ボルトねじ部の相当応力(この場合、ねじ山の応力集中を含まない公称応力です)が、材料の降伏応力の70〜90[%]程度の値となるようなトルクを締結トルクとして決めることが多いようです。被締結体に作用させることができる繰り返し荷重は、軸力が大きいほど大きくなります。つまり、締結トルクが大きいほど強度的に有利となり、締結トルクがゼロになると許容できる繰り返し荷重はかなり小さくなります。
参考文献:
- [1]日本規格協会|ねじの締め付け通則 JIS B 1083|(2008)
内力係数φのおさらい
図3にボルト締結体に繰り返し荷重Fが作用している状態を示します。ボルトの初期締結トルクがゼロのときのボルトねじ部に発生する応力は荷重÷断面積で、応力振幅σa0はその半分ですね。次式で表されます。
ねじ部の断面は、図4に示したようにらせん溝が切られた軸の断面なので円形ではありません。ねじ有効径を直径とする円の面積より小さく、谷径を直径とする円の面積より大きいので、式5と式6が使われています。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

 式1
式1 式2
式2
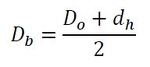 式3
式3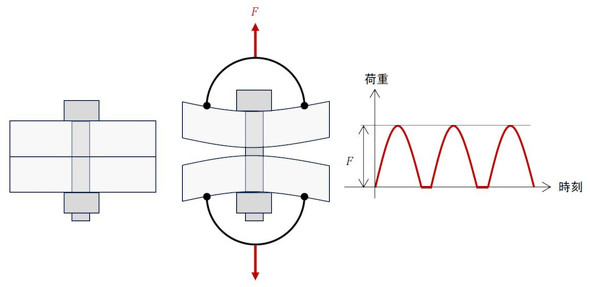
 式4
式4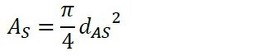 式5
式5 式6
式6