「ねじ締結体」を理解する:CAEを正しく使い疲労強度計算と有機的につなげる(14)(3/4 ページ)
有限要素法による計算例:締め付けトルクと軸力
ここから、ボルトの疲労破断の有無の予測方法について説明していきますが、筆者は実験環境を持ち合わせていないのでシミュレーションを使います。「実験しなくてシミュレーションだけで大丈夫?」というご意見もあるかと思いますので、シミュレーション結果がボルトに関する理論式の通りになるかを確認しましょう。締め付けトルクと軸力の関係式である式1と式2を使って、シミュレーションの計算精度を確認します。
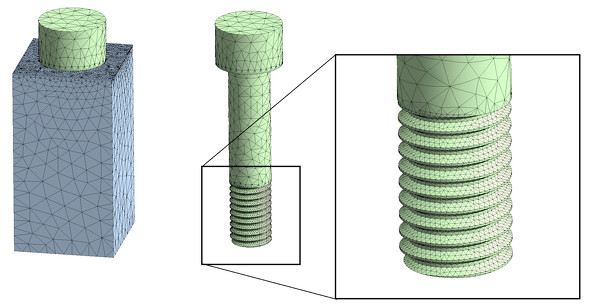
らせんねじを切ったボルトとナットをモデリングします。図10に示す手順でモデリングしました。
3D CADを使います。図10において(1)のように円柱をモデリングします。ここで使った3D CADはねじ山のモデリング機能があったので(2)のように簡単にねじ山ができました。このような機能がない場合は三角形断面を定義して、らせん状に掃引することになります。(3)と(4)で円柱を追加してボルトが出来上がりました。(5)は単に直方体を追加しただけです。(6)は物体のブーリアン演算で、これでめねじができました。(7)ではボルト穴の方の直径を少し広げています。これをSTEP形式でファイル出力して有限要素法ソフトに読み込みます。図11に要素分割図を示します。
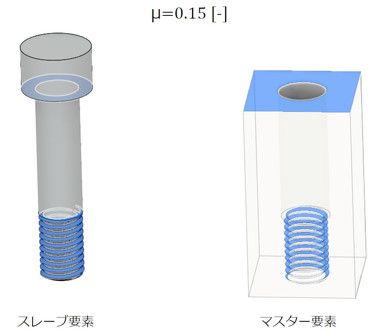
次に接触要素の設定です。以前説明したように、接触要素は物体の表面に配置します。図12に接触要素を示します。ボルトのねじ山とボルトの頭にスレーブ要素を、被締結体のねじ山とボルト頭との接触面にマスター要素を配置しました。
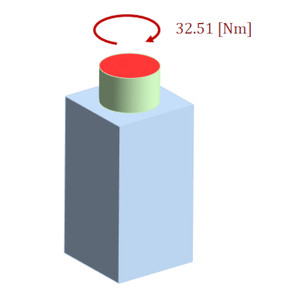
続いてトルク荷重を設定します。図13に示すように、右ねじの進む方向に32.51[Nm]のモーメント荷重を設定します。有限要素法ソフトでは「微小変形問題」がデフォルト設定になっているので「大変形問題」に変えて計算します。
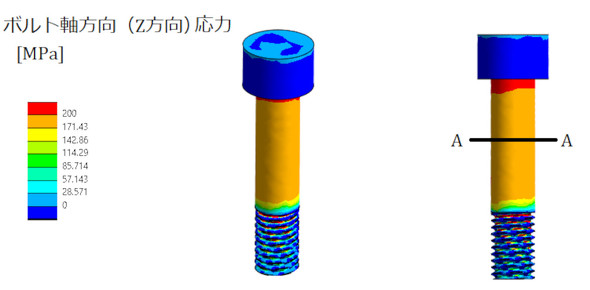
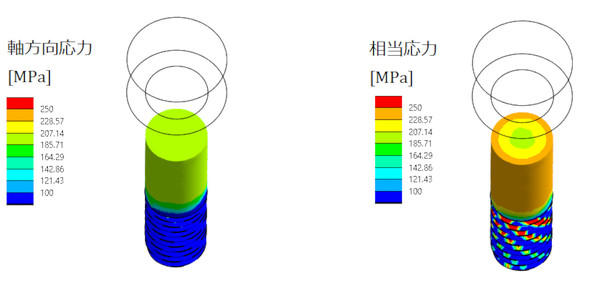
図14にボルトの軸方向応力分布を示します。図14のA-A断面にある節点の応力値をテキストファイルに出力し、平均すると197[MPa]となりました。
図15にA-A断面の応力分布を示します。ボルトの軸部にはねじりトルクが発生しているので、相当応力は軸の外側が大きくなっています。
次は理論式です。摩擦係数を0.15[-]とし、M10の諸元を式2に代入するとトルク係数は以下の値になりました。
ボルトに発生する軸力は、式1を変形して以下となります。
軸力をA-A断面の断面積で割ります。
理論式による値とシミュレーション値を比較したものを表1に示します。理論式との差は3.3[%]と良い感じに一致しました。シミュレーション結果を信用しても問題なさそうですが、あと1つ検証してみましょう。
| 単位 | 理論式 | シミュレーション | 差 | |
|---|---|---|---|---|
| 締め付けトルク | Nm | 32.51 | 32.51 | − |
| 軸力 | N | 15996 | 15475 | 3.3% |
| 軸方向応力 | Pa | 204 | 197 | 3.3% |
| 表1 ボルトに発生する軸方向応力 | ||||
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞


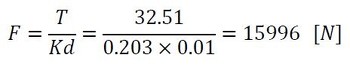 式18
式18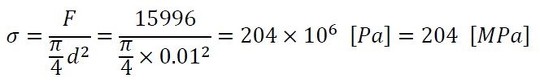 式19
式19





