ボルト締結体のシミュレーションについて考える：CAEを正しく使い疲労強度計算と有機的につなげる（16）（1/4 ページ）
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第16回では「ボルト締結体のシミュレーション」について取り上げる。
連載第14回で、内力係数φを説明しました。ボルトに発生する応力振幅は、単純に計算した「荷重／断面積の半分」のφ倍、つまり「荷重／断面積の半分」の数分の1になります。このことをシミュレーションに反映させるにはボルトの初期締結力をシミュレーション内で発生させる必要があります。この方法を説明します。
ボルトの初期締結力を発生させる：簡単な例
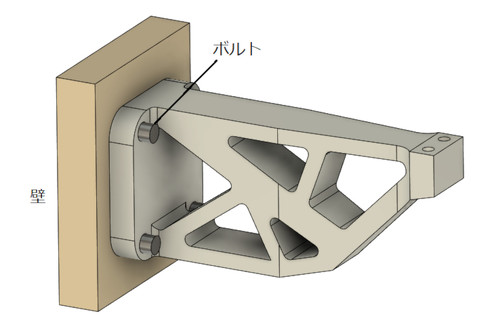
連載第1回で紹介したブラケットを使って簡単な例を説明します。図1に、壁に固定されたブラケットを示します。壁は大きな部品で壁側の強度計算はしないことが前提で、強度計算の対象はボルトとブラケット本体となります。
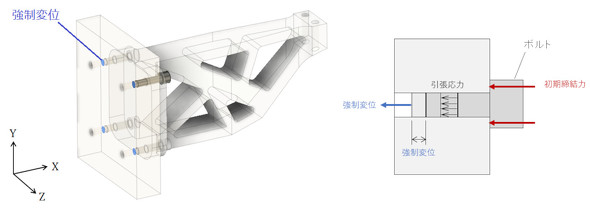
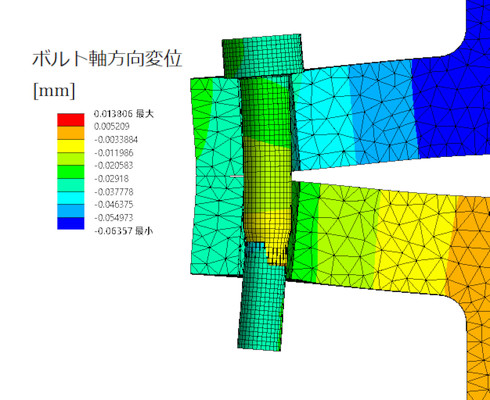
初期締結力を発生させるためには、図2に示すようにボルトの先端に強制変位を与えます。ボルトには引張応力が発生し、引張応力にボルトの有効断面積を掛けた値が初期締結力となって、この力でボルトの頭がブラケットを押し付けます。
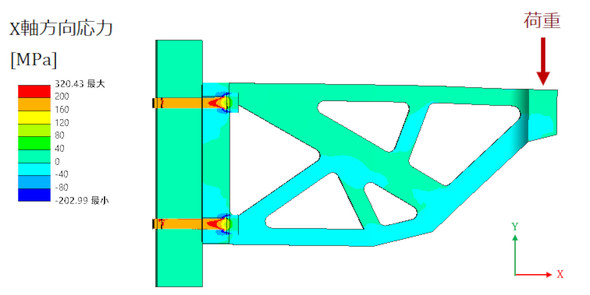
目標応力は、ボルトの軸力を有効断面積で割った値となります。M10ボルトの場合、ボルトの直径は10［mm］ではなく、有効断面積に応じた直径（有効径と谷径の平均値）でモデリングするところがポイントです。ボルト断面のボルト軸方向応力（X軸方向応力）をテキストファイルで出力し、「Excel」で平均値を出します。これが目標応力になるまで強制変位量を調整します。3回くらい計算すれば目標応力になると思います。
ボルトに発生する応力振幅は、荷重を掛けたときのボルトの応力と、荷重を掛けないときのボルトの応力との差の半分ですね。図2で強制変位を設定せずに荷重を設定すると、前述した応力振幅がゼロという結果になるので注意してください。
ボルトの初期締結力を発生させる：一般的な例
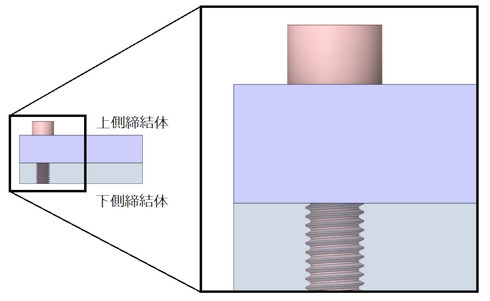
では、図4に示すように、ボルト、上側被締結体、下側被締結体が強度評価対象となる場合はどうしましょうか。今度は強制変位が使えませんね。
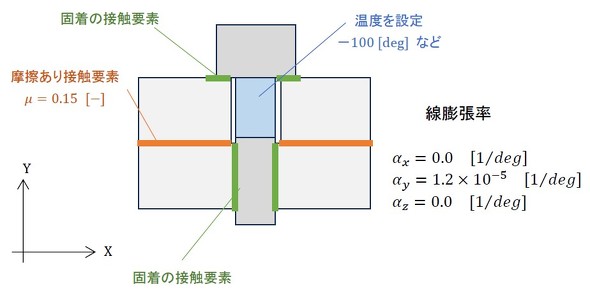
方法は2つあります。一つは熱収縮を使う方法です。図5に示すように、ボルトを冷却して引張応力を発生させます。ボルトの材質で「直交異方性の線膨張率」を設定する必要があります。ボルトの軸方向の線膨張率を適当な値とし、それ以外の方向の線膨張率をゼロとします。
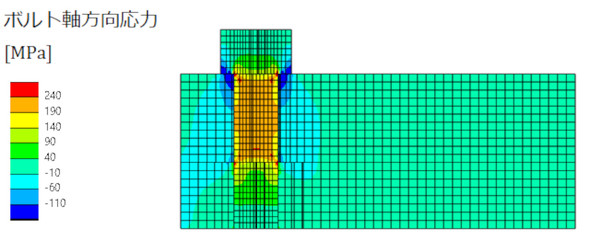
図6に熱収縮させた状態を示します。ボルトは164［deg］程度冷却しております。ボルト側に引張応力（197［MPa］）、被締結体側に圧縮応力が発生しています。
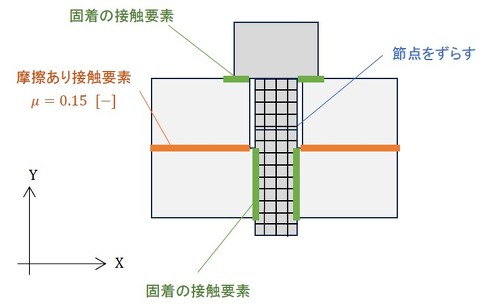
もう一つは、Ansysのボルトプリテンション機能を使います。ボルトプリテンション機能の内部は公開されていないので筆者の推測が少し混じりますが、図7で示すように、目標とする軸力になるように節点をずらしているようです。
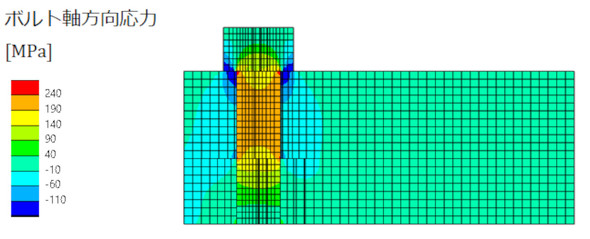
図8にボルトプリテンション機能を使った状態を示します。節点位置が少しずれていて、ボルト側に引張応力、被締結体側圧縮応力が発生しています。
図9にボルトプリテンション機能を使った別の例を示します。変位量を拡大すると、節点がずれていることが分かります。ボルトプリテンション機能を知らない方にこのような図を使って説明すると誤解を招く場合があるので、普段は節点がずれていることが気付きにくい図にして説明しています。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
ITmediaはアイティメディア株式会社の登録商標です。