ボルト締結体のシミュレーションについて考える:CAEを正しく使い疲労強度計算と有機的につなげる(16)(3/4 ページ)
ボルトの軸力決定方法
シミュレーションで再現させるボルトの軸力について説明したいと思います。連載第14回で述べたトルク係数で計算するのですが、これからかなり差し引く必要があります。軸力を差し引く要因として、以下のものが考えられます。
- 締め付けトルクのばらつき
- 機械の稼働によってボルト近傍が揺すられて起きる力の再配分
- スパナを外したときの軸力低下
- 被締結体のクリープ変形
「締め付けトルクのばらつき」について考えます。締め付け係数Qというものがあって、式1で定義されています。
締め付け時のボルトねじ部の相当応力が降伏応力の70〜90[%]程度になるような条件で締め付けトルクを決めたときは「弾性域の締め付け」と呼びます。トルクレンチを使ってこの締め付けトルクで締め付けた場合の締め付け係数は1.4〜3[-]程度です(参考文献[1])。軸力がばらつくので、ばらつきの範囲の最小値を見積もります。
締め付け係数が3[-]だとします。この場合、軸力は例えば1000〜3000[N]の範囲でばらつきます。3倍もばらつくため、たまたま軸力が高くなったケースではボルトが降伏しているでしょう。そうすると、軸力が1000[N]になったケースでのボルトに発生する応力は降伏応力の3分の1、つまり33[%]となります。一方、締結時の応力の設計値は降伏応力の70[%]とすると、ボルトの軸力による応力は、設計値(70[%])が33[%]まで下がったので、設計値の約2分の1ですね。ばらつきの範囲の軸力最小値は設計値の約半分ということになりますが、この推定はかなり強引でした。
過去の連載記事「設計者向けCAEを使ったボルト締結部の設計」で摩擦係数を紹介しましたが、2倍程度のばらつきの範囲があったので、前述した約半分というのはあり得ると考えられます。ボルト疲労破断の有無の予測のためのシミュレーションでは悪い状態を想定するので、軸力は設計値の半分以下となります。まだ他にも軸力を低下させる要因があります。
参考文献:
- [1]日本規格協会|ねじの締付け通則|JIS B1083(2022)
機械の稼働による軸力低下
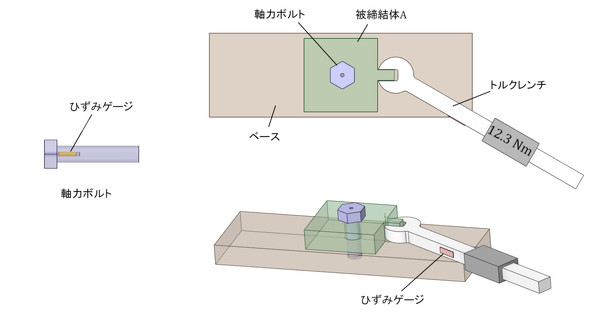
「機械の稼働によってボルト近傍が揺すられて起きる力の再配分」による軸力低下ですが、被締結体の表面の凹凸がつぶれることが原因の一つだといわれています。実験をしてみました。実験装置を図17に示します(写真はご容赦ください)。
軸力ボルトは中にひずみゲージが埋め込まれていて、ボルトに軸力が作用するとボルトの軸が伸びて、そのときのひずみ量が測定できます。ひずみ値から軸力を計算します。「機械の稼働によってボルト近傍が揺すられる」ことの模擬として、図17の右図に示すように被締結体を5[deg]ほど回転させて、また元に戻しました。
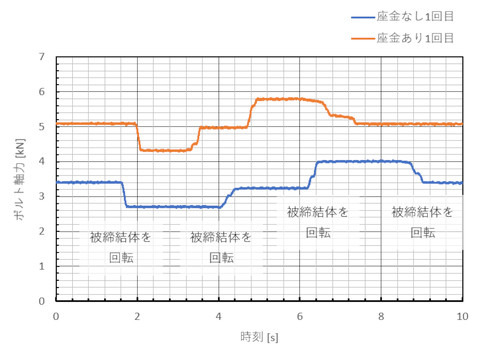
図18にボルト軸力の変化を示します。オレンジ色の線は座金を使わない条件でのボルト軸力、青色の線は座金を使った条件でのボルト軸力変化です。被締結体の回転とともにボルトも回転し軸力が上下しましたが、回転位置を元に戻すと同じ軸力に戻りました。つまり、軸力は低下しませんでした。
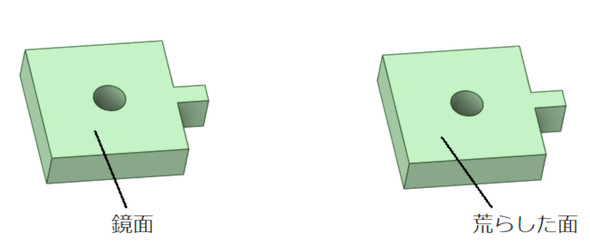
図19に被締結体の表面を示します。図17の試験は左側です。このような図面指示ではなかったのですが、被締結体の表面はほぼ鏡面でした。
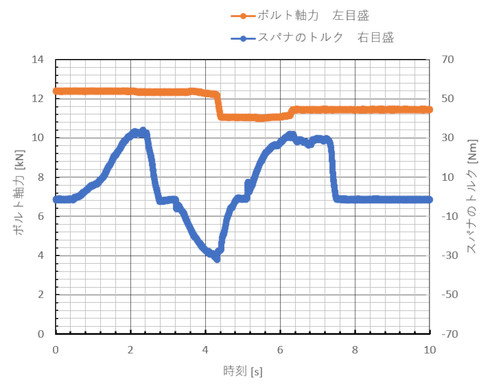
今度は、被締結体の表面を荒らして同じ試験をしました。図20に軸力を示します。
今度は、被締結体を回転させてもボルトは一緒に回りませんでした。オレンジ色の線がボルト軸力ですが、面荒らしをした被締結体を使うとボルト軸力が低下しました。この実験は「被締結体の表面の凹凸がつぶれる」との説明を裏付ける結果となりました。今度はスパナのトルクも測定しました。
では、どれくらいの軸力低下を見積もればよいでしょうか。ボルト近傍がこれ以上ないというくらいに揺すられた映像がYouTubeにありました。ユンカー緩み試験機による映像です。この映像の中に緩まなかったナットがあります。このときの軸力曲線から軸力低下は20[%]程度だと推定されます。機械稼働による軸力低下の上限は20[%]と考えられます。これ以上の軸力低下はねじの緩み発生と捉えた方がよく、別の対策が必要となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞

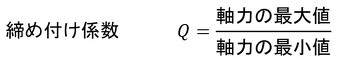 式1
式1