ボルト締結体のシミュレーションについて考える：CAEを正しく使い疲労強度計算と有機的につなげる（16）（2/4 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

ボルトが締め付けられた状態での応力振幅

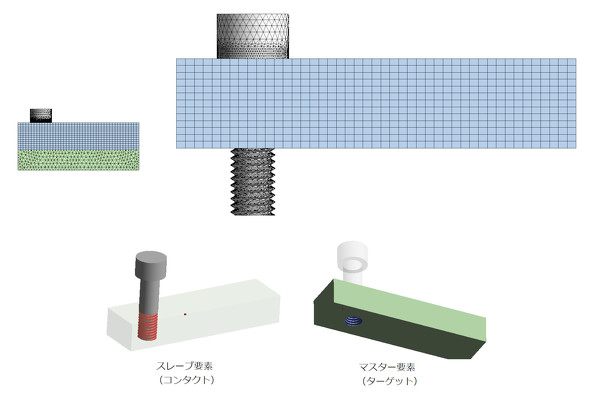
　ボルトの疲労破断の有無を予測するには、ボルトが締め付けられた状態での応力振幅を求める必要があります。応力振幅は前述した2つの方法で正しく求まるでしょうか。比較してみましょう。比較する相手は、らせんねじを切ったボルトをシミュレーションの中で回転させて軸力を発生させたモデルです。この解析結果を“正”とします。解析モデルを図10に、初期締結状態を図11に示します。ボルトは10.3［deg］回転させました。

図10　解析モデル：らせんねじ方式［クリックで拡大］

図11　ボルトに発生させた初期締結力：らせんねじ方式［クリックで拡大］

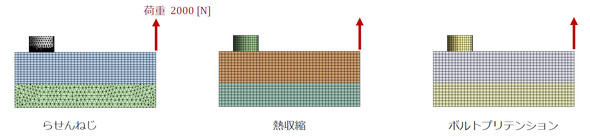
　図12に解析モデルと荷重条件を示します。普通、ボルトの軸と荷重が同一線上になることはないので偏心荷重としました。3つのモデルに同じ荷重を掛けてボルトに発生する応力振幅を比較してみましょう。

図12　解析モデルと荷重条件［クリックで拡大］

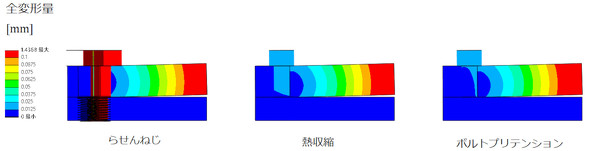
　図13に3者の変位量を示します。大変形問題として計算していますが、ボルトの頭が膨らんでいます。大きな回転が生じたときの「あるある挙動」ですね。

図13　変形量［クリックで拡大］

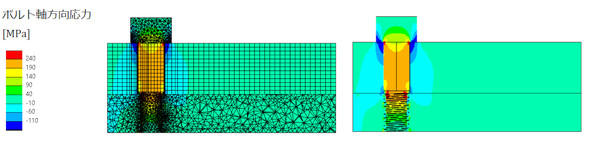
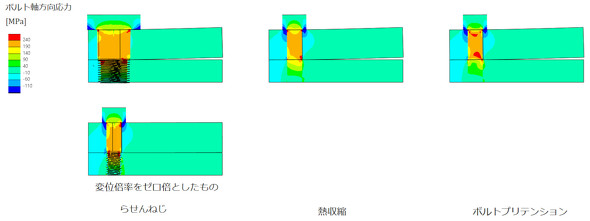
　図14にボルト軸方向応力分布を示します。らせんねじではボルト本体も膨らんで見づらいので、変位倍率をゼロとしたものを併記しました。色を見る限り同じ応力が発生しました。

図14　ボルト軸方向応力［クリックで拡大］

　ボルトに発生する応力振幅を求めましょう。図15にボルト軸断面の応力分布を、表1に応力振幅を示します。

図15　ボルト軸方向応力［クリックで拡大］

	単位	らせんねじ	熱収縮	ボルトプリテンション
平均応力	MPa	196	197	197
最大応力	MPa	224	222	223
応力振幅	MPa	14	13	13
表1　ボルトに発生する応力振幅

　らせんねじ方式、熱収縮方式、ボルトプリテンション方式による応力振幅はほぼ同じ値となりました。らせんねじを用いた応力振幅を“正”とすると、熱収縮方式とボルトプリテンション方式はボルトの応力振幅を求めるのに有効な方法といえます。よって、ボルトの疲労破断の有無の予測に必要とするCAEソフトの仕様は以下となります。

• 接触要素が使えること
• 直交異方性の線膨張率を設定できること

　ないしは、

• ボルトプリテンション機能があること

　かなり高額なソフトの仕様となりました。フリーのFEM（有限要素法）ソフト「LISA」でできる簡易的な方法を考える必要がありますね。

異方性でなく等方性の線膨張率を使った場合

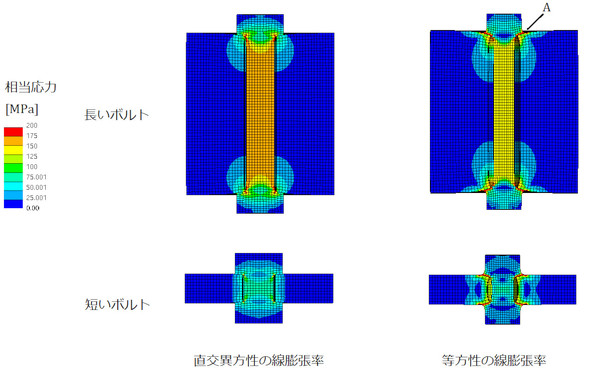
　「直交異方性の線膨張率を設定できること」という仕様はハードルが高いので、等方性の線膨張率の設定でできないかを調べましょう。等方性の線膨張率とは普通の線膨張率のことです。図16に直交異方性の線膨張率を使ったときと、等方性の線膨張率を使ったときの相当応力分布を示します。

図16　直交異方性の線膨張率と等方性の線膨張率の比較［クリックで拡大］

　等方性の線膨張率ではボルトが半径方向に縮んでしまい、少し見栄えが悪くなります。図16のA部に高応力部が発生しますが、これくらいは目をつぶりましょう。ボルトが長い場合は、ボルト中央部は均一な応力なので使えそうです。応力を示す色が左図はオレンジ、右図は黄色と異なりますが、冷却する温度を調整することで所望の初期締結力を出せます。筆者もボルトが長い場合は等方性の線膨張率で済ませることがあります。しかし、ボルトが短い場合はボルト軸部の均一な応力領域があまりないので、ボルトに曲げが作用するときに等方性の線膨張率を使うには無理がありそうです。