ボルト締結体に作用できる許容繰り返し荷重:CAEを正しく使い疲労強度計算と有機的につなげる(17)(3/4 ページ)
有限要素法なしで許容繰り返し荷重を計算できないだろうか
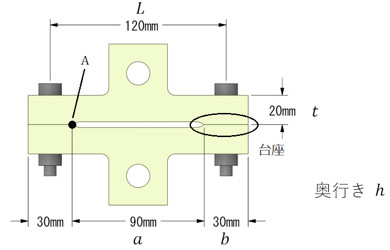
有限要素法を使わずに、紙と鉛筆で許容荷重を求めることはできないでしょうか。少し検討してみましょう。図9のような形状をモチーフとします。台座が追加されています。台座の追加で強度は向上しないのですが、考察を進める上で必要なため追加しました。
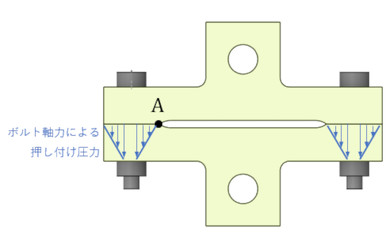
ボルトが2本のときは、ボルトに曲げ応力が発生するため、ボルトに発生する応力振幅が大きくなりました。ということは、図9のA点が密着していればボルトが曲げられることがなく、曲げ応力が抑えられます。「A点が開口しないこと」を強度計算の指標にしてはどうでしょうか。では、A点が開口しない条件を紙と鉛筆で求めてみましょう。
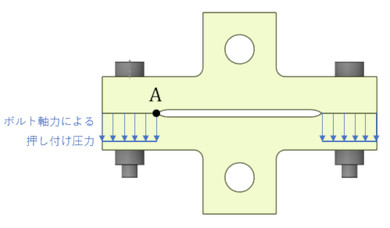
図10に、ボルトの締結力によって締結体が押し付けている圧力を示します。圧力分布は一様と仮定しました。
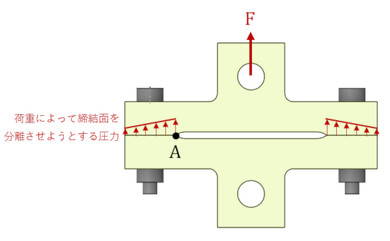
次に、荷重によって図10の圧力の分布がどれだけ減少するかを考えます。図11に、荷重によって締結面を分離させようとする圧力分布を示します。締結面には曲げモーメントが発生するので図のような圧力分布としました。図10の圧力分布から図11の圧力分布を差し引いた圧力が、荷重時の締結面同士の接触圧力となります。A点の圧力がプラスだとA点は接触、つまり開口しないことになり、ボルトは大丈夫だと判断できます。
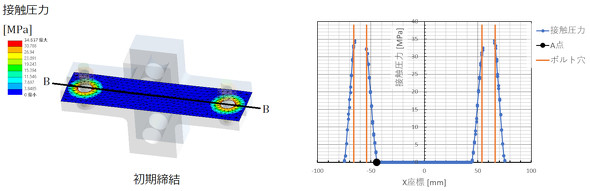
図10のボルトの締結体が押し付けている圧力をもう少し詳しく調べてみましょう。図12左図に初期締結時の接触圧力分部を示します。被締結体の接触面のうちB−B線上の接触圧力を図12右図に示します。図12は初期締結状態で荷重を掛けていません。
A点でちょうど接触圧力がゼロになってしまいました。ボルトの締結力によって締結体が押し付けている力の分布は図10ではなくて、図13のようです。最初からA点の接触圧力がゼロなので、これから図11に示した荷重によって締結体が引っ張られる圧力を引き算すると必ずマイナス値になり、A点は常に開口するとの結果となりました。
紙と鉛筆では「ダメだこりゃ」っていうことを書きました。ここでは開口を判定する位置が適切ではなかったと思います。接触圧力分布が計算できるハイスペックなCAEソフトを使わず、フリーソフトである「LISA」でボルトの疲労破断の有無を予測する方法を考えなければなりません。前述した考察から以下のヒントが得られました。
- 開口位置をA点ではなく無理やり決めて、「開口しないこと」を疲労破断しない条件とできないだろうか
- 開口の有無を固定点の反力で判定できないだろうか
- 開口の有無を無理やり決めた開口位置近傍の応力で判定できないだろうか
次回、上記の考察について進めていくことにします。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査