【問題10】 NANDゲートは“万能ゲート”:完全マスター! 電子回路ドリル II(10)
「論理演算の定理」を適用して、同じ機能を持つ回路を“もっと少ないゲートで構成する方法”について詳しく解説します。
【問題9】の解答
前回の宿題【問題9】は、「多数決回路」をできるだけ少ないゲートで作成するという問題でした。
皆さん解けましたでしょうか?
解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。
それでは、解答を発表します!
【問題9】の解説
最初に、【問題7】の解説で説明した真理値表から論理式を導く方法を用いて、【問題9】のデジタル回路を作ってみましょう。
真理値表の出力が“1”の行に注目して、次のように論理式を求めます。
X = A ・ B ・ C + A ・ B ・ C + A ・ B ・ C + A ・ B ・ C
この論理式を回路にすると図1のようになります。
【問題9】では「同じ機能を持つ回路を、もっと少ないゲートで構成できないか?」を問うています。そこで、中学校で習う「式の変形」のように論理式を変形し、同じ応答をするより簡単な論理式を求めてみましょう。
論理式の変形は、次のような「論理演算の定理」を適用して行います。
復元の法則
二重否定すると、その値は元に戻ります。
=
A = A
冪(べき)等の法則
値自体を論理和(あるいは論理積)しても結果は同じになります。
A + A = A A ・ A = A
相補の法則
ある論理変数とそれを否定したものの論理和は“1(真)”になり、ある論理変数とそれを否定したものの論理積は“0(偽)”になります。
A + A = 1 A ・ A = 0
恒等の法則
論理和と論理積には、次のような性質があります。
A + 0 = A A ・ 0 = 0
A + 1 = 1 A ・ 1 = A
交換の法則
論理和と論理積の左辺と右辺を入れ替えても結果は同じです。
A + B = B + A A ・ B = B ・ A
結合の法則
論理和と論理積は、演算を評価する順番にかかわらず同じ結果になります。
(A + B) + C = A + (B + C) (A ・ B) ・ C = A ・ (B ・ C)
分配の法則
論理和は論理積に対して分配的であり、論理積は論理和に対して分配的です。
A + (B ・ C) = (A + B) ・ (A + C) A ・ (B + C) = (A ・ B) + (A ・ C)
吸収の法則
論理式が積の和の形で表され、すべての因数となる項を含むとき、その項に式を省略することができます。論理式が和の積の形で表される場合も同様です。
A + (A ・ B) = A A ・ (A + B) = A
ド・モルガンの法則
ド・モルガンの法則により、論理和を論理積に、論理積を論理和に変換できます。
A + B = A ・ B A ・ B = A + B
それでは、これらの論理演算の定理を適用して、先に求めた「多数決回路」の論理式を簡単にしてみましょう。
X = A ・ B ・ C + A ・ B ・ C + A ・ B ・ C + A ・ B ・ C
は「冪等の法則」により、
X = (A ・ B ・ C + A ・ B ・ C) + (A ・ B ・ C + A ・ B ・ C) + (A ・ B ・ C + A ・ B ・ C)
と展開できます。
さらに、この式は「分配の法則」により、
X = B ・ C ・ (A + A) + A ・ C ・ (B + B) + A ・ B ・ (C + C)
とまとめられます。
そして、「相補の法則」により、
X = B ・ C + A ・ C + A ・ B
と簡単化できます。
この論理式を基に作成した「多数決回路」が図2となります。
このように図1よりも少ないゲートで回路を実現することができます。
次回までの宿題 ― 【問題10】
- デジタル回路よ永遠なれ−2学期【期末考査】解答編
- フリップフロップとその応用 〜2学期【期末考査】〜
- デジタル回路の総仕上げ! 【期末考査】のお知らせ
- 【問題20】 グレイ・コード・カウンタの設計
- 【問題19】 N進同期カウンタの設計
- 【問題18】 カルノー図によるカウンタ回路の設計
- 【問題17】 非同期カウンタと同期カウンタ
- 【問題16】 D-FFでカウンタを作る
- 【問題15】 D-FFによるシフトレジスタ
- 【問題14】 JK-FFのタイムチャート
- 【問題13】 SR-FFのタイムチャート
- 【問題12】 フリップフロップの動作
- 中間考査解答編&【問題11】タイムチャート
- 基数変換とゲート回路の設計 〜2学期【中間考査】〜
- 知識の点検、2学期【中間考査】のお知らせ
- 【問題10】 NANDゲートは“万能ゲート”
- 【問題9】 ゲート回路の簡単化
- 【問題8】 真理値表から加算回路を作る
- 【問題7】 真理値表からゲート回路を作る
- 【問題6】 論理式からゲート回路へ
- 【問題5】 組み合わせ論理回路
- 【問題4】 符号付き2進数と符号なし2進数
- 【問題3】 負の数の2進表現
- 【問題2】 2進数の加減算と乗算
- 【問題1】 数の表現「10進数と2進数」
関連記事
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- 急成長中の中国ヒューマノイド大手AgiBotの技術戦略
- 光通信入門事始め――古代の人々ののろしと同じように光で信号を送ってみよう
- イチから全部作ってみよう(29)3つのノート整理法からたどるRDBMSの基礎知識
- AIスパコンやロボット活用で「稼げる農業」へ、農研機構と東京工科大が連携協定
- 宇宙用途向け耐放射線FPGAが欧州の宇宙用部品規格の認定を取得
- OKIエンジが北関東校正センターを設立「計測器校正は第三者校正が主流に」
- デジタルツイン向けマルチLiDAR異常検知技術を開発
- IIJの法人モバイル契約数が350万回線に、マルチプロファイルSIM2.0の特許も取得
- IoTゲートウェイの課題はデータの欠損と変換、IIJ子会社が新コンセプトで解決へ
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【前編】
コーナーリンク
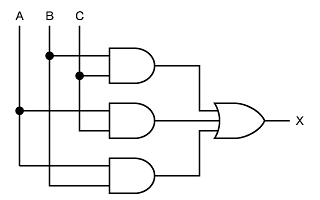
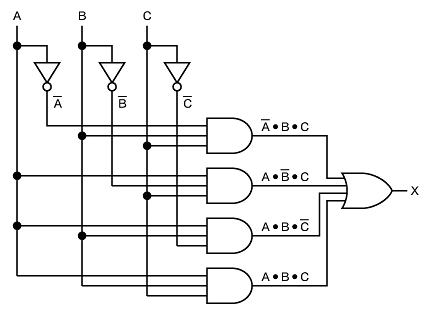 図1 多数決回路(その1)
図1 多数決回路(その1)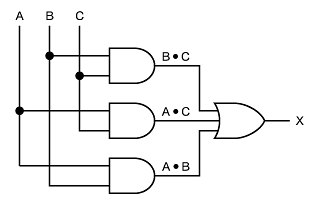 図2 多数決回路(その2)
図2 多数決回路(その2)

