【問題4】 符号付き2進数と符号なし2進数:完全マスター! 電子回路ドリル II(4)
「high」と「low」のいわゆる“ビットデータ”で表現されるデジタル回路の世界で、負の数をどのように扱えばよいのでしょうか?
【問題3】の解答
前回の宿題【問題3】は、“負の数の2進表現”に関する問題でした。皆さん解けましたでしょうか?
解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。
それでは、解答を発表します!
問題3
「−5」を2進数で表すと? 8ビットの2の補数で表してください。
答え.(11111011)2
【問題3】の解説
【問題3】は2進数で負の数をどのように取り扱うかという問題です。
われわれが負の数を扱うとき、−5のように「−(マイナス記号)」を数の前に付けて表します。しかし、デジタル回路では、H(high)とL(low)のいわゆるビットデータしか扱うことができません。
ここで負の数のビット表現を考えてみましょう。
「ある負の数と対応する正の数の和は“ゼロ”」です。従って−5では、
5 + ( −5 ) = 0
という式が成り立ちます。
これを基に、−5の2進数(ビット表現)を考えると、
( 101 )2 + ( x )2 = 0
となり、「x」の部分が−5に相当します。
以上を踏まえたうえで、詳しい解説に入りますが、先に【問題3】の答えを明かします。
答えは「(11111011)2」です。
では、この答えで本当に「5 + ( −5 ) = 0」が成立するかどうかを確認してみましょう。
図1の計算式を見ると、最上位にけた上がりが生じますが、続く8ビットはゼロになり「5 + ( −5 ) = 0」の計算が成り立ちます。
以上のような負の数の表現方法を「2の補数表現」といい、2の補数は2進数の加減算に適合することからコンピュータの世界でよく使われます。
それではここで、2の補数の求め方について解説します。
最初に対応する正の数を2進数に変換します。−5の場合、5を2進数に変換します。これを8ビットで表現すると、
5 = (00000101)2
となります。
次に、各ビットの「0」を「1」に、「1」を「0」に反転させます。すると
(11111010)2
となります。
最後に、これに「1」(つまり「(00000001)2」)を加えれば終了です(図2)。
図2から−5は「(11111011)2」と求められます。
次回までの宿題 ― 【問題4】
- デジタル回路よ永遠なれ−2学期【期末考査】解答編
- フリップフロップとその応用 〜2学期【期末考査】〜
- デジタル回路の総仕上げ! 【期末考査】のお知らせ
- 【問題20】 グレイ・コード・カウンタの設計
- 【問題19】 N進同期カウンタの設計
- 【問題18】 カルノー図によるカウンタ回路の設計
- 【問題17】 非同期カウンタと同期カウンタ
- 【問題16】 D-FFでカウンタを作る
- 【問題15】 D-FFによるシフトレジスタ
- 【問題14】 JK-FFのタイムチャート
- 【問題13】 SR-FFのタイムチャート
- 【問題12】 フリップフロップの動作
- 中間考査解答編&【問題11】タイムチャート
- 基数変換とゲート回路の設計 〜2学期【中間考査】〜
- 知識の点検、2学期【中間考査】のお知らせ
- 【問題10】 NANDゲートは“万能ゲート”
- 【問題9】 ゲート回路の簡単化
- 【問題8】 真理値表から加算回路を作る
- 【問題7】 真理値表からゲート回路を作る
- 【問題6】 論理式からゲート回路へ
- 【問題5】 組み合わせ論理回路
- 【問題4】 符号付き2進数と符号なし2進数
- 【問題3】 負の数の2進表現
- 【問題2】 2進数の加減算と乗算
- 【問題1】 数の表現「10進数と2進数」
関連記事
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- イチから全部作ってみよう(29)3つのノート整理法からたどるRDBMSの基礎知識
- 月面を照らす「光の物差し」 JAXAとカシオが可視光測位技術を実証
- 東芝の2つの次世代ゲート駆動技術がSiCデバイスの損失削減に寄与、ISSCCで発表
- NXPがエッジへのAIエージェント実装を推進、数百TOPSクラスの新たなNPUも開発へ
- AUTOSARの“AR”はアーキテクチャに由来、アーキテクチャ設計にどう使うのか
- 買い物客の8割が求める「自分だけの割引」、小売業はどう対応すべきか
- クレーンゲームにIoTデバイスを搭載しスマホ決済、新店の約370台に搭載
- インフィニオンがams OSRAMのセンサー事業を買収、自動車や医療向けを強化
- TFT技術とメタマテリアル技術を融合した衛星アンテナ用基板を共同開発
- 非安全なコントロールアクション「UCA」の書き方
コーナーリンク
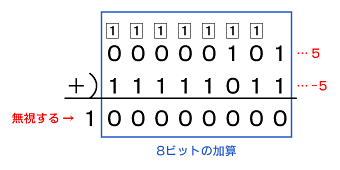 図1 8ビットがゼロになることを確認
図1 8ビットがゼロになることを確認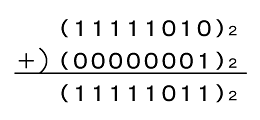 図2 2の補数の求め方
図2 2の補数の求め方

