中間考査解答編&【問題11】タイムチャート:完全マスター! 電子回路ドリル II(13)
2学期【中間考査】の解答を発表します! 基数変換やゲート回路の設計をテーマにした問題の数々、皆さんはいくつ解けましたか?
前回行った2学期【中間考査】では、“基数変換”や“ゲート回路の設計”の問題を中心に出題しました。いかがでしたでしょうか?
解けた方も解けなかった方も、次項の解答と解説をぜひ読んでみてください。
仮に解けなかった問題があったとしても、今回の解説や過去問題を参考にして、1問1問確実に理解しながら解いていけば、必ずやその知識が身に付くはずです。
それでは、解答を発表します!
中間考査−第1問の解答と解説
第1問
答え.
| 10進数 | 2進数 | 16進数 | |
| 100 | 1100100 | 64 | |
| 50 | 110010 | 32 | |
| 250 | 11111010 | FA | |
10進数と2進数の変換については、【問題1】の解説を参考にすれば解ける問題です。ここでは、連載で触れていなかった「16進数(Hexadecimal Number)」について解説します。
16進数とは、
- 「0」「1」「2」「3」「4」「5」「6」「7」「8」「9」「A」「B」「C」「D」「E」「F」の16種類の数字で表す
- 基数が16である
数をいいます。
16進数による数の表記には16種類の文字が必要なので、「0」から「1」の数字に加え、「A」から「F」までの英字を用います。ここで「A」は10を表し、「B」は11を表し……、「F」は15を表しています。
そして、16進数のけたの重さは1(160)の位、16(161)の位、256(162)の位……のように、1つけたが上がるたびに16倍になります。
つまり、16進数の「FA」を10進数に変換するには、図1のようにけたの重みを考えて、
15 × 16 + 10 × 1 = 240 + 10 = 250
と求めます。
続いて、16進数と2進数との関係ですが、
- 16進数の1けたは、2進数の4けたに相当
します。
つまり、2進数「1100100」を16進数に変換するには、図2のように2進数を4けたずつ分けて行います。
一方、16進数「FA」を2進数に変換する場合は、図3のように16進数の各けたを、4けたの2進数に置き換えて行います。
このように、16進数でビットを表現すると非常にコンパクトになります。
中間考査−第2問の解答と解説
これら3つの問題については【問題6】の解説を参考にすれば、論理式から回路を導き出せます。しかしながら、同じ機能であってもさまざまな回路が考えられますので、ここでは“より最適な回路”について考えてみましょう。
(2)の解答を見てください。これは論理式をそのままゲートに置き換えたものですが、この論理式を、
X = A + B ( C + D ) = A + B ・ C + B ・ D
と変形することで、図4のようにさらに応答のよい回路が実現できます(参考【問題9】の解説)。
同じく(3)の解答ですが、こちらの論理式は、
X = A ( B + C ) + A ・ B = A ・ B + A ・ C + A ・ B = A ・ B + A ・ C
と簡単化できます。これにより、少ないゲートで回路を実現できます(参考【問題9】の解説)。
中間考査−第3問の解答と解説
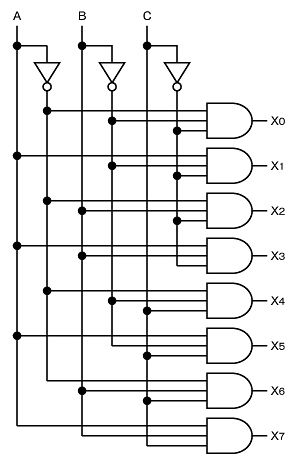
第3問は、真理値表から回路を求める問題です。はじめに、真理値表から論理式を求め、そこからゲート回路を作成していきます。【問題7】の解説のとおり、「真理値表の出力が“1”となる行の基本積を求め、それらの論理和を取る」方法を利用します。
この方法により求められる「3‐8デコーダ」の論理式は以下のとおりです。
- X0 = A ・ B ・ C
- X1 = A ・ B ・ C
- X2 = A ・ B ・ C
- X3 = A ・ B ・ C
- X4 = A ・ B ・ C
- X5 = A ・ B ・ C
- X6 = A ・ B ・ C
- X7 = A ・ B ・ C
後は、これらを基にゲート回路を描けば答えが導き出せます。
中間考査−第4問の解答と解説
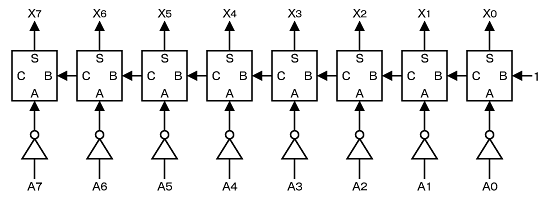
ここでは解答例として、【問題8】の解説で紹介した「HA(Half Adder:半加算器)」を8個並べて実現してみました。
【問題3】の解説のとおり、ある2進数の補数は「各ビットを反転(否定)し、1を加える」ことで求められます。そこで、HAの入力Aに各けたのビットを反転したものを加え、HAの入力Bにより1を加算するためのキャリーCを伝達させています。
前述しましたが、デジタル回路を作る際、その解答は必ずしも1つとは限りません。同じ機能であっても、応答性、回路規模、電気特性などさまざまな検討を要することがあります。1つの問題の解答に、いくつかのバリエーションを発見することもデジタル回路ならではの面白さだと筆者は思います。ご興味があればぜひチャレンジしてみてください。
以上で、2学期の中間考査の解答と解説は終了です。お疲れさまでした。
最後に、次回までの宿題を掲載します。
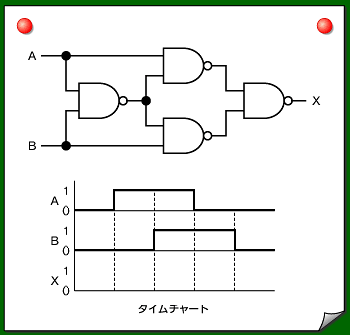
次回までの宿題 ― 【問題11】
- デジタル回路よ永遠なれ−2学期【期末考査】解答編
- フリップフロップとその応用 〜2学期【期末考査】〜
- デジタル回路の総仕上げ! 【期末考査】のお知らせ
- 【問題20】 グレイ・コード・カウンタの設計
- 【問題19】 N進同期カウンタの設計
- 【問題18】 カルノー図によるカウンタ回路の設計
- 【問題17】 非同期カウンタと同期カウンタ
- 【問題16】 D-FFでカウンタを作る
- 【問題15】 D-FFによるシフトレジスタ
- 【問題14】 JK-FFのタイムチャート
- 【問題13】 SR-FFのタイムチャート
- 【問題12】 フリップフロップの動作
- 中間考査解答編&【問題11】タイムチャート
- 基数変換とゲート回路の設計 〜2学期【中間考査】〜
- 知識の点検、2学期【中間考査】のお知らせ
- 【問題10】 NANDゲートは“万能ゲート”
- 【問題9】 ゲート回路の簡単化
- 【問題8】 真理値表から加算回路を作る
- 【問題7】 真理値表からゲート回路を作る
- 【問題6】 論理式からゲート回路へ
- 【問題5】 組み合わせ論理回路
- 【問題4】 符号付き2進数と符号なし2進数
- 【問題3】 負の数の2進表現
- 【問題2】 2進数の加減算と乗算
- 【問題1】 数の表現「10進数と2進数」
関連記事
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- 急成長中の中国ヒューマノイド大手AgiBotの技術戦略
- 光通信入門事始め――古代の人々ののろしと同じように光で信号を送ってみよう
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【前編】
- 宇宙用途向け耐放射線FPGAが欧州の宇宙用部品規格の認定を取得
- AIスパコンやロボット活用で「稼げる農業」へ、農研機構と東京工科大が連携協定
- OKIエンジが北関東校正センターを設立「計測器校正は第三者校正が主流に」
- IIJの法人モバイル契約数が350万回線に、マルチプロファイルSIM2.0の特許も取得
- イチから全部作ってみよう(29)3つのノート整理法からたどるRDBMSの基礎知識
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- IoTゲートウェイの課題はデータの欠損と変換、IIJ子会社が新コンセプトで解決へ
コーナーリンク
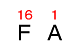 図1 16進数とけたの重み
図1 16進数とけたの重み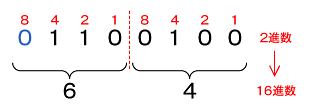 図2 2進−16進変換
図2 2進−16進変換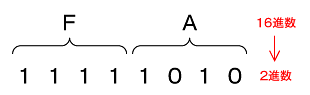 図3 16進−2進変換
図3 16進−2進変換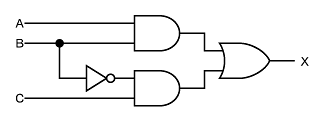
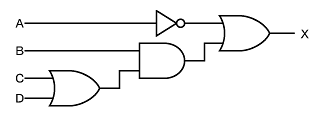
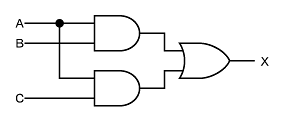
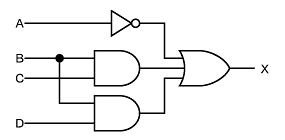 図4 (2)の解答(その2)
図4 (2)の解答(その2)