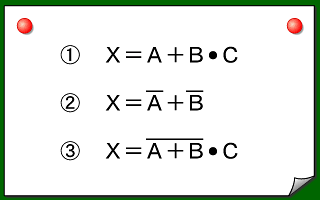【問題6】 論理式からゲート回路へ:完全マスター! 電子回路ドリル II(6)
論理演算を行う回路素子“ゲート”について解説。デジタル回路の働きを調べるには「信号の流れを入力から順番に見ていくこと」です。
【問題5】の解答
前回の宿題【問題5】は、3つの基本論理演算である「AND」「OR」「NOT」を組み合わせて作った回路の論理機能を調べる問題でした。
皆さん解けましたでしょうか?
解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。
それでは、解答を発表します!
【問題5】の解説
最初に論理演算を行う回路素子、「ゲート(gate)」について説明します。
ANDゲート
AND演算を行う回路素子を「ANDゲート」といいます。ANDゲートは「複数の入力がすべて“1”であるとき“1”を、それ以外は“0”を出力」します。
ANDゲートは、図1のように四角形と半円を組み合わせたような記号で表します。
ORゲート
OR演算を行う回路素子を「ORゲート」といいます。ORゲートは「複数の入力に1つでも“1”があったならば“1”を、それ以外は“0”を出力」します。
ORゲートは、図2のように三日月のような(出力部分はとがらせる)記号で表します。
NOTゲート
NOT演算を行う回路素子を「NOTゲート」といいます。NOTゲートは「入力が“0”のとき“1”を、入力が“1”のとき“0”を出力」します。また、NOTゲートは「インバータ(inverter)」とも呼ばれます。
NOTゲートは、図3のように三角形と小さい円からなる記号で表します。
以上がゲートの解説となります。
解説した3つのゲートの働きが分かったところで、【問題5】を解いてみましょう。
デジタル回路の働きを調べるには、「信号の流れを入力から順番に見ていく」ことがポイントとなります。
そこで、図4のようにゲート1(ANDゲート)の出力をD、ゲート2(NOTゲート)の出力をEとして順番に調べていきます(ゲート1とゲート2はどちらを先に調べてもよい)。
信号Dは、入力Aと入力Bがともに“1”のとき“1”を、ほかの場合は“0”を出力します。
信号Eは、入力Cが“0”のとき“1”を、“1”のとき“0”を出力します。
最後に出力Xは、信号Dと信号Eのどちらか1つでも“1”であれば“1”となり、図4の回路の真理値表は以下のようになります(表1)。
次回までの宿題 ― 【問題6】
- デジタル回路よ永遠なれ−2学期【期末考査】解答編
- フリップフロップとその応用 〜2学期【期末考査】〜
- デジタル回路の総仕上げ! 【期末考査】のお知らせ
- 【問題20】 グレイ・コード・カウンタの設計
- 【問題19】 N進同期カウンタの設計
- 【問題18】 カルノー図によるカウンタ回路の設計
- 【問題17】 非同期カウンタと同期カウンタ
- 【問題16】 D-FFでカウンタを作る
- 【問題15】 D-FFによるシフトレジスタ
- 【問題14】 JK-FFのタイムチャート
- 【問題13】 SR-FFのタイムチャート
- 【問題12】 フリップフロップの動作
- 中間考査解答編&【問題11】タイムチャート
- 基数変換とゲート回路の設計 〜2学期【中間考査】〜
- 知識の点検、2学期【中間考査】のお知らせ
- 【問題10】 NANDゲートは“万能ゲート”
- 【問題9】 ゲート回路の簡単化
- 【問題8】 真理値表から加算回路を作る
- 【問題7】 真理値表からゲート回路を作る
- 【問題6】 論理式からゲート回路へ
- 【問題5】 組み合わせ論理回路
- 【問題4】 符号付き2進数と符号なし2進数
- 【問題3】 負の数の2進表現
- 【問題2】 2進数の加減算と乗算
- 【問題1】 数の表現「10進数と2進数」
関連記事
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【後編】
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- ルネサスが「Renesas 365」を提供開始、電子機器の開発期間を大幅短縮
- 出荷量1.3倍を実現、電源不要のIoTゲートウェイが南種子町にもたらす農業改革
- チップレットでASIL Dを支援する車載SoC技術を開発
- 光量子コンピュータ実用化に向けた「10dBの壁」を突破、誤り耐性の獲得にも寄与
コーナーリンク
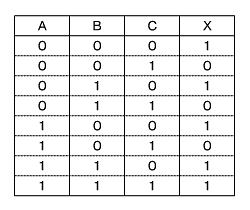
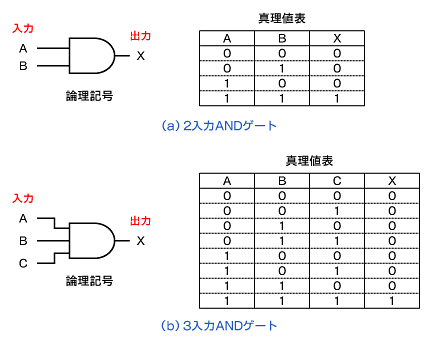 図1 ANDゲートの記号と真理値表
図1 ANDゲートの記号と真理値表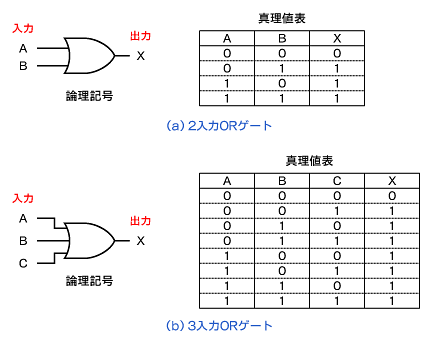 図2 ORゲートの記号と真理値表
図2 ORゲートの記号と真理値表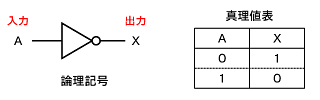 図3 NOTゲートの記号と真理値表
図3 NOTゲートの記号と真理値表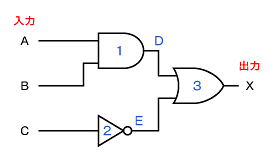 図4 回路各部の信号
図4 回路各部の信号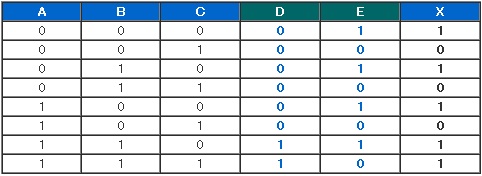 表1 【問題5】の真理値表
表1 【問題5】の真理値表