制御設計の基本! ボード線図を極めよ:独学! 機械設計者のための自動制御入門(9)(4/4 ページ)
前ページで、銀二さんのいったことを説明します。
まず1+τ・sのボード線図のグラフの全体像を把握することから始めましょう。そのために、ゲイン曲線、位相曲線のグラフの両端がどうなるかということを考えます。 例えばω→0のときは、位相θについては、(17)からtanθ=τ・ω→0、ゲインについては、(16)から10・log(1+(τ・ω)2)→0です。従ってω→0では位相θもゲインも→0となります。つまりωが0近くの低周波数域では位相もゲインも0に収束します。
次にω→∞では、(17)からtanθ=τ・ω→∞ですから、位相θは90°に収束します。一方ゲインは(16)から→∞です。つまりゲインは10・log(1+(τ・ω)2)→∞に発散します。従ってωが無限大近くの高周波域では位相θは90°、ゲインは∞となるわけです。 これで、位相曲線、ゲイン曲線の両端の様子が分かりました。それでは、それ以外の周波数域での様子はどうでしょうか。
まず中間の周波数域の特別な周波数の場合について考えてみましょう。ω=1/τのときは(17)からtanθ=1ですから、ω=1/τのとき位相θは45°進んでいることが分かります。そしてゲインは(16)から
次に、ωが0から1/τの間ではどうなるでしょうか。tanθ=τ・ω、τω<1ですから位相θはωに比例して0から45°まで単調に増加することが分かります。ゲインはですから0から3dBまで単調に増加します。ただしゲイン10・log(1+(τ・ω)2)はわずか3dBしか増加しませんから、ほとんど0(dB)のままということがいえます。 最後にωが1/τから無限大の間ですが、位相θは45°を越えて周波数ωとともに単調に増加します。ただし最初に説明したように90°を超えることはありません。
ゲインも周波数ωとともに単調に増加しますがω>1/τでは、
ですから、ゲイン曲線は横軸log(ω)に対して、勾配20の直線に漸近することが分かります。
以上のように一次進み要素1+τ・sのボード線図は、位相曲線は「S字曲線」、ゲイン曲線は「折れ線」となり、ボード線図は図9のように描くことができます。ここではこのようなボード線図の作図法を「簡易作図法」と呼ぶことにします。なお、位相曲線の勾配はω=1/τで最大となり66°/decadeとなります。詳しく知りたい人は補足資料(jido09.pdf)を参照してください。
なるほどね。この作図法だと のτとグラフの関係がよく分かるね。僕がエクセルで計算したボード線図に、おじさんが説明してくれたことを書き加えると図10のようになるね
図10を見てなんか気がつかへんか?
同じ形状のグラフがτに応じて横方向に平行移動しているね
ということは1+τ・sの伝達関数のボード線図は1+sのボード線図をテンプレートとして描くことができるっちゅうことや。つまり1+τ・sの位相曲線は1+sの位相曲線をω=1/τで45°の点を通るように平行移動すればいいということやな。同様に、1+τ・sのゲイン曲線は1+sのゲイン曲線をω=1/τで0(dB)の点を通るように平行移動すればいい。ほんとうはω=1/τで3(dB)の点を通過するんやけど、簡易作図だから、大胆にω≪1/τで0(dB)としてもええやろ
次に1/(1+τ・s)の伝達関数のボード線図やけど、これは図9の赤線で示すように(1+τ・s)の伝達関数のボード線図を上下に折り曲げたものになる。なぜ、そうなるかは後で自分で確認しといてや
は〜い。分かりました。1+τ・sは周波数ωとともに位相が進むから一次進み要素、1/(1+τ・s)は位相が遅れるから一次遅れ要素と呼ぶんだね
それじゃ、いま説明した簡易作図法で(3)のGPIと(4)のGPIDのボード線図を描いてみようか。第7回の図9はエクセルで描いたPI制御のボード線図やから、まずそれを描いてくれへん?
第7回のコントローラG1の式(28)を書き直すと
となるから、G1は比例 と積分 と の掛け算だ。 第7回の図9は、KP=c=2で、KI=b=0.1だった。この場合について計算すると
1+τ・sのボード線図のゲイン曲線は図11の点線に示すように、1+sのボード線図のゲイン曲線(青線)を平行移動して、折れ点をω=1/τ=0.05に合わせ、折れ点を基点として20°/decadeの右肩上がりの折れ線を描けばいい
1+τ・sに1/2を掛けるというのは、1+τ・sのゲイン曲線に図6の積分1/sのゲイン曲線を足すことになるから、黒細線と黒点線を足すと1/(1+τ・s)のゲイン曲線は図11の黒線になる。これってω=1を中心に点線を回転させたように見えるね
そうやな。おもろい見方をするな。そういう感性って大事やで
最後に比例要素K1を掛けると、(1+τ・s)/sのゲイン曲線が20(dB)下に下がる。それがK1(1+τ・s)/sのゲイン曲線で図11の赤線がそうだよ。第7回の図9でB=0.1のときのゲイン曲線と比較すると大体一致していることが分かるね
そうやな。1+τ・sの位相曲線は1+sの曲線をω=0.05で45°を通るように平行移動してやればいいし、それをさらに90°下げたのが(1+τ・s)/sの位相曲線だ。比例要素 を掛けても位相は変わらんから、結局図11の赤線がK1(1+τ・s)/sの位相曲線だ
なるほどね。第7回の図9は叔父さんがエクセルで描いたのをいきなり見せられたので正直ついていけなかったけど、こうして自分で手で描いてみると納得感が湧いてくるね
そうや。人は誰でも経験したことしか理解できひん。『分かる』というのは、自分の手足と頭を使って何かをしたときに感じる現実感、つまり過去に経験して得られた知識を使って予測したことと、実際に起こったこと、やったことが一致するときに感じる納得感だと思うんや。だから『分かる』ためには、自分の手と足と頭を使わなあかんねん……
おじさん、足は何に使うん?
あほ! …… じゃあ次は、(4)のGPIDのボード線図を描いてみようか
おじさんゴメン。もう帰らなくちゃ。新幹線の時間が迫ってる。毎晩、お母さんから電話がかかってきて、『いつまでおじさんのところで遊んでるの! 早く帰っておいで!』 ってうるさいんだ。だから、一度うちに帰るよ。またすぐ戻ってくるから、続きを教えてね
な、何やと!
草太はそういい残すと、そそくさとおじさんの書斎を出ていきました。しかし荷物は残したままです。本当に、またすぐ戻ってくるようです。どうやら草太も明石海峡を望めることができるこの町が気に入ったようですね。
次回は、最初にコントローラG1を、PI制御にDを加えてPID制御にしたときのG1のボード線図の簡易作図法について再び学習します。その後、前回(第8回)問題となった自動走行制御システムの応答の悪さ、がPID制御によりどのように改善されるかを説明します。そして、シミュレーションを使ってPID制御の効果を検証し、ボード線図を使う設計方法がいかに有効かを確認します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
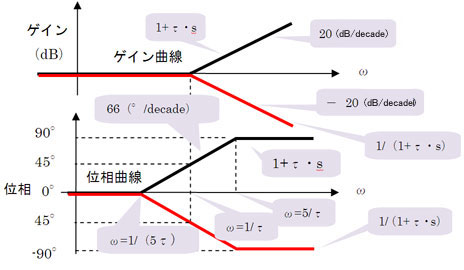 図9 簡易作図法による1+τ・s(一次進み要素)と1/(1+τ・s)(一次遅れ要素)のボード線図
図9 簡易作図法による1+τ・s(一次進み要素)と1/(1+τ・s)(一次遅れ要素)のボード線図 
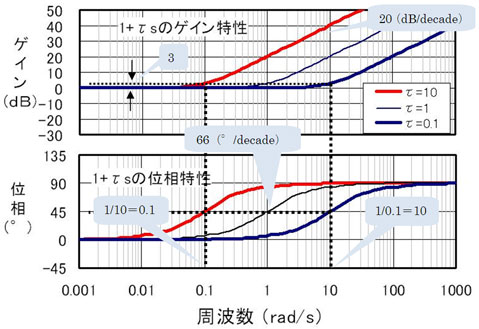 図10 エクセルで作成した一次進み要素 のボード線図
図10 エクセルで作成した一次進み要素 のボード線図 


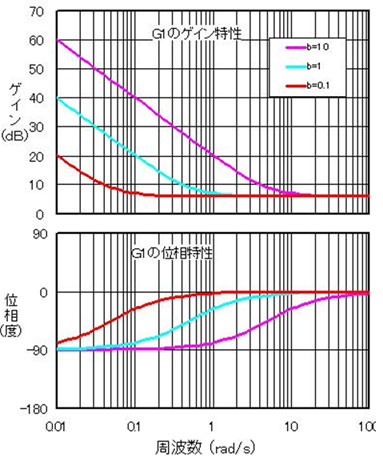 第7回 図9
第7回 図9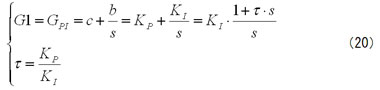
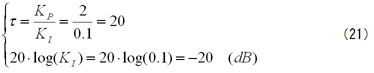
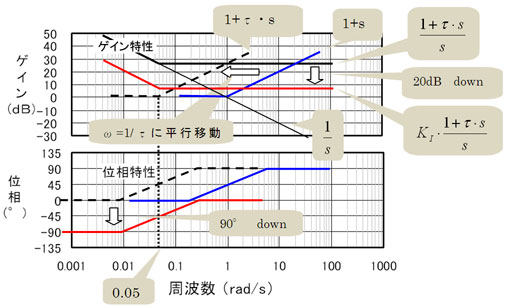 図11 簡易作図による第7回の図9(PI制御のコントローラG1のボード線図)
図11 簡易作図による第7回の図9(PI制御のコントローラG1のボード線図) 








