ラプラス変換と割り切ったお付き合いをするよ:独学! 機械設計者のための自動制御入門(6)(1/4 ページ)
草太が制御工学の単位を落とす原因を作った、憎き「ラプラス変換」。でも“道具”だと割り切って使えば、そんなに難しくないのだ
当連載の登場人物
銀二(ぎんじ)
設計コンサルタント。甥(おい)っ子の草太を自分の息子のようにかわいがっています。
草太(そうた)
銀二の甥。現在は大学院生です。ちょっと困るとすぐ叔父を頼ってしまうちゃっかり者だけど、頑張り屋さんです。
編集部注* 本記事はフィクションです。実在の人物団体などとは一切関係ありません。
前回は、横風を受けて曲がる自動車を真っすぐ運転させる自動運転制御の代わりに、もっと分かりやすい、水漏れのあるお風呂の浴槽の水位制御の方法について考えました。浴槽の水位制御の場合、目標水位hoと実際の水位hの差(偏差)hに比例したバルブ開度xとする比例制御では、水漏れがあると水位hを目標水位hoまで到達させることはできないことが分かりました。水漏れQに相当するお湯を補充するためのバルブ開度xを維持するためには、目標水位hoとの偏差hが0であってはならないからです。そこで、偏差hが0となっても、漏れ流量Qに相当するバルブの開度xを維持させるために、偏差hを積分する制御を考えてみました。しかし、水位hは目標水位hoを中心にして変動するだけで、一向に目標水位に落ち着きません。図1に示す、積分制御による浴槽水位制御の開ループシステムの位相余裕が0°なので、システムが不安定となるからです。
今回も、瀬戸内海の風香る銀二叔父さんの書斎から始まります。位相余裕を増やして、システムを安定化する方法について説明します。それによって、積分の効果を有効なものとすることができます。
そうか、開ループの位相余裕は0°だから、ループを閉じたとき、システムは発振するんだ。第3回で聞いた話の重要さがいま分かったよ
システムが安定なのか、不安定なのか、という判断は非常に重要やで
そうだね
じゃあ、不安定を安定にするにはどうしたええと思う?
位相余裕やゲイン余裕を大きくすればいいんだよね
具体的にどうする?
図1のブロック線図の『バルブ−流量特性』の伝達関数G2、浴槽水位特性の伝達関数G3の周波数応答特性(ボード線図)は変えられそうにないから、バルブモータコントローラの伝達関数G1の周波数応答特性を変えるんだろうね
だろうな。で、どうする?
図2の開ループシステムの伝達関数Goの周波数応答特性(ボード線図)を見ると、ゲインが0(dB:デシベル)を切る周波数は1(rad/min:ラジアン毎分)で、そのときの位相遅れが180°。この180°の遅れを、とにかくもっと小さくできればいいんだよね
そういうことやねん
どうするん?
自分で考えろや! ……っていいたいけど、ヒントを出してやろうか。偏差hを積分するってのは、いわば過去の情報を使ってバルブの開度xを制御しようってことやろ? 過去の情報の積み重ねを利用するわけだから、その情報には当然遅れがある。その遅れが位相遅れ180°となってシステムが不安定となっているんや。だから、過去の情報だけでなく、現在の情報も加えて制御してやればいいんや
叔父さんのいってる『現在の情報で制御する』というのは、比例制御のことだよね。でも比例制御では、目標水位には制御できなかったよね……
そうや。現在の情報だけではうまくいかん。つまり現在を刹那(せつな)的に生きている若造だけでやってもうまくいかん。そこで、年寄りが経験した過去の知識を使って制御しようとしたが、年寄りは動きが遅くて、これもうまくいかへん。だから、経験豊富な年寄りと動きの速い若造を一緒にして協力しながら仕事をさせたらうまくいくんとちゃうの? っちゅうことやな
なんか、よく分からないな。で、どうするん?
つまり、バルブモータコントローラの伝達関数G1を、比例と積分を足し合わせたものにしてみたらどうや? っていうこと。そのときのG1の周波数応答特性、つまりボード線図の位相特性が前より改善されていれば、安定性も改善されるはずや
そうやろな。こんな計算やってられへんよな。しゃーないな。ここで、あれを出そうか
うん? なにが出るの?
ラプラス変換や!
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞


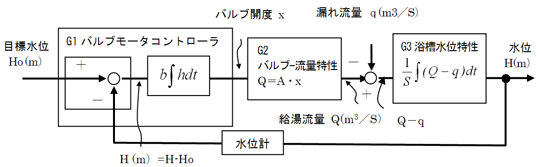 図1 積分制御による浴槽水位制御
図1 積分制御による浴槽水位制御 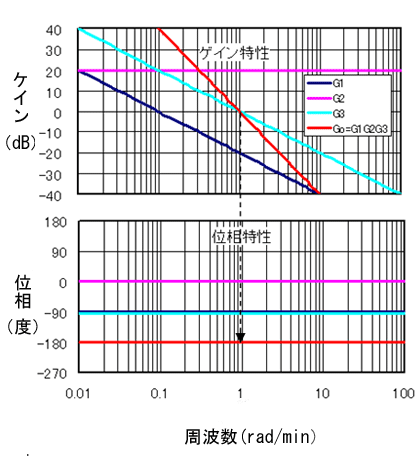 図2 積分補償による浴槽水位制御システムの ボード線図
図2 積分補償による浴槽水位制御システムの ボード線図 








