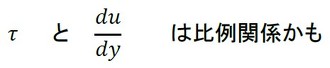ニュートン流体とパイプ内の層流:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(9)(1/4 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第9回は、ニュートン流体とパイプ内の層流をテーマに取り上げる。
これまでの内容で、固体内部の熱伝導部の温度差(Tmax−Tmin)よりも、伝熱界面における壁温度と主流(流体)温度との熱伝達部の差(Twall−T∞)の方が、はるかに大きいことを示してきました。
ヒートシンクがその典型例です。ということは、伝熱界面の熱伝達率を精度よく求める必要があります。しかし、熱伝達率の計算はかなり難しく、公式に当てはめて計算できる対象は、円形パイプ内の流れ、円柱周りの流れ、垂直平板、水平円板などに限られます。
本シリーズでは“紙と鉛筆”による計算と“CAE”による結果を比較しやすい題材として、円形パイプ内の流れや円柱周りの流れに取り組みます。
流体の流速が速いほどよく冷えることから、流速分布を知ることや、どれだけの圧力をかけたら所望の流速が得られるかを知るために、パイプの入り口圧力と流量の関係を計算することは、冷却系の設計において不可欠です。まずは熱流体解析に先立って、流体解析について解説していきます。
ニュートン流体
私たちが日常的に接している空気や水は「ニュートン流体」に分類されます。連載第3回では、熱伝達に関する「ニュートンの近似」について説明しました。「近似」としたのは、予測精度がそれほど高くないからです。ニュートン流体に関しては、近似ではなく「ニュートンの粘性法則」が適用され、かなり高い精度で実験結果と一致します。
では、ニュートン流体の定義について説明します。この定義は、流体の粘性係数の定義にもなっています。ニュートン流体では、式1が成立します。
もちろん、x方向とy方向は直交しています。流速uを座標 yで微分しており、これを「速度勾配」と呼びます。普段、手を洗ったり、風が顔に当たったりしたときに感じるのは、主に流体の衝突による力(動圧)であり、「流体の粘性」を実感できる場面は多くありません。そこで、「水あめ」を使って実験をしてみましょう。動画1をご覧ください。
図1に実験装置を示します。この装置は、水あめに浮かんでいる板を、おもりの重力によって引っ張ろうとするものです。映像の前半では重いおもりを使用したため、板は速く移動しました。後半では、軽いおもり(緑色)を用いたため、板の移動はゆっくりになりました。
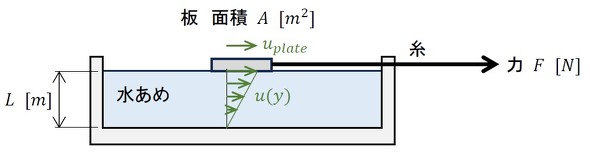
図2に板の速度と板に作用する力を示します。板の加速は終了し、一定速度uplateになっているようです。水あめと板の間に滑りがないようなので、uplateは水あめの水面の速度と一致します。
水あめの水深をL[m]とし、水あめの水平方向速度をy座標の関数とすると、u(L)=uplateと表せます。一方、水底の速度はゼロなので、u(0)=0です。2点の流速の情報しかありませんが、この2点を直線で結ぶと図2のような速度分布が描けます。今、勝手に直線で結びましたが、平行2平板間の層流は線形となるため問題はありません。
板が一定速度であるということは、力の釣り合いが成立しており、板が水あめから受ける力と、おもりによる力が等しいことを意味します。板が水あめから受ける力は、明らかに水平方向の力であり、式2でせん断応力が定義されます。
動画1では、重いおもりを使用した場合の方が、板の速度が速くなっていました。つまり、Fが大きいほど、uplateも大きくなります。また、流速uの分布を直線で表したため、uの座標yによる微分も大きくなります。以下のような感じでしょうか。
これらを踏まえると、以下のような関係が推測されます。
本当に比例関係があるとして、その比例定数を粘性係数μとしたものが、ニュートン流体となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

 式1
式1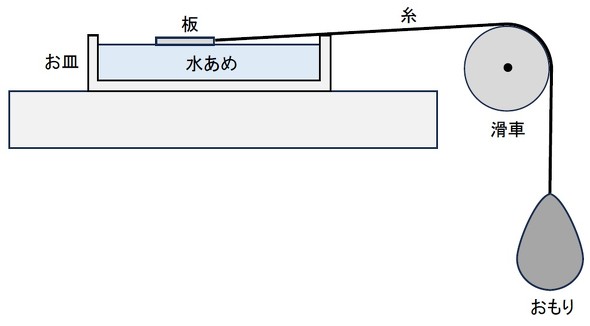
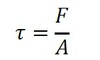 式2
式2