ニュートン流体とパイプ内の層流:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(9)(3/4 ページ)
円管内流れの微分方程式の検算
さて、式8は正しいのでしょうか。これを確認するために「ナビエ・ストークス(Navier-Stokes)」式と比較してみましょう。ナビエ・ストークス式は次式で表されます(参考文献[1])。
円筒座標系におけるナビエ・ストークス式では、速度の記号が以下のように変わります。
式9の左辺の演算子は式11です。
今回の問題では、流れに時間変化がないため、式11の右辺第1項はゼロになります。次に、Vr=Vθ=0であるため、第2項および第3項もゼロです。さらに、z座標が変わっても流速分布が変化しないため、第4項もゼロになります。よって、式9の左辺はゼロとなります。
式9のラプラス演算子∇2は、円筒座標系では式12となります。なお、円筒座標系における軸方向はz方向ですが、図5での軸方向はxなので表記を変えます。
Vr=0、Vθ=0、さらに外力ベクトルもゼロであるため、式9の軸方向成分は式13として表されます。
流速uは、角度θと流れの方向に対して一定値であるため、結局式12は次のようになります(式14)。
圧力はxだけの関数で、流速uは半径だけの関数なので、偏微分記号を微分記号に変えます。そして、μ=ρνの関係式を用います。
おおっ! 式8と一致しました。計算に誤りはなかったようです。
参考文献:
- [1]生井武文、井上雅弘|機械工学基礎講座 粘性流体の力学|理工学社(1978)
円管内流れの速度分布
では、式8を解いてみましょう。とはいえ、この微分方程式を筆者の力で解くのは難しいため、カンニングします。参考文献[2]によると、式8の一般解は式16となります。
この一般解を微分すると、速度勾配は式17で表されます。
境界条件から積分定数を求めます。中心上では対称性から、せん断応力はゼロになります。これは、円筒座標系においてマイナスの半径という概念がなく、半径ゼロの位置では、発生したせん断力を支える相手が存在しないためです。このことから、式18が成立します。
式18を式16に代入すると、積分定数C1はゼロになります。
パイプ壁面の流速はゼロなので、式19が成立します。
式19を式16に代入すると、積分定数C2は式20となります。
積分定数を式16に代入すると、速度分布は式21で表されます。
この速度分布は放物線になりますね。中心の流速を求めるときは、r=0を代入しますが、これでは流速がマイナス値になりそうです。しかし、圧力勾配dp/dx(※2)がマイナス値であるため、結果として流速はプラス値となります。つまり、圧力が下がる方向に流体が流れることを意味します。同様に、熱伝導の場合も温度が下がる方向に熱が伝わりましたよね。
参考文献:
- [2]日本機械学会|機械工学便覧 A5 流体工学|(1992)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

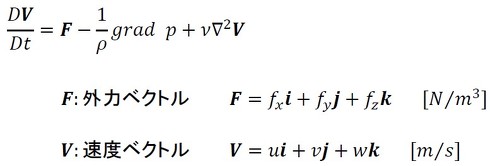 式9
式9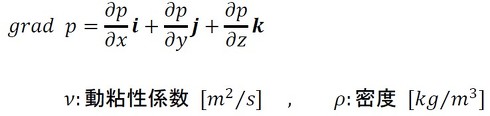 式10
式10
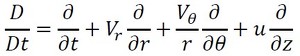 式11
式11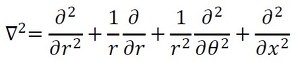 式12
式12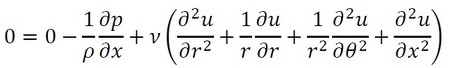 式13
式13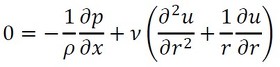 式14
式14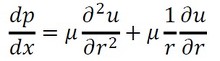 式15
式15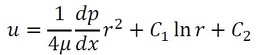 式16
式16 式17
式17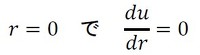 式18
式18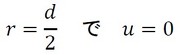 式19
式19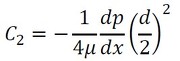 式20
式20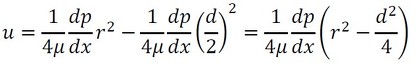 式21
式21