ニュートン流体とパイプ内の層流:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(9)(2/4 ページ)
円管内流れの微分方程式
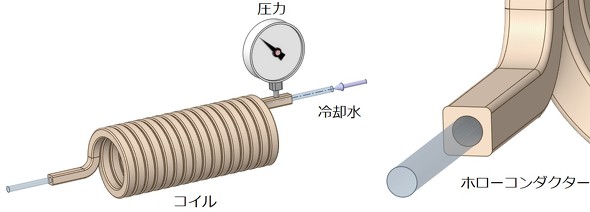
連載第1回で、「ホローコンダクター」を使ったコイルを紹介しました(図3)。ここでの最終目標は「ホローコンダクターの温度を、絶縁材がダメージを受けない範囲にすること」ですが、まずは「必要とする冷却水の流量を確保できる入り口圧力を求めること」を当面の目標にしましょう。
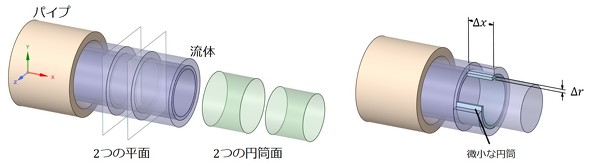
図4に円形パイプ内を流れる流体の様子を示します。図4左図のように、流体を2つの平面と2つの円筒面で分割します。すると、図4右図のように、厚さΔr、長さΔxの微小な円筒が出来上がります。この微小な円筒に注目します。
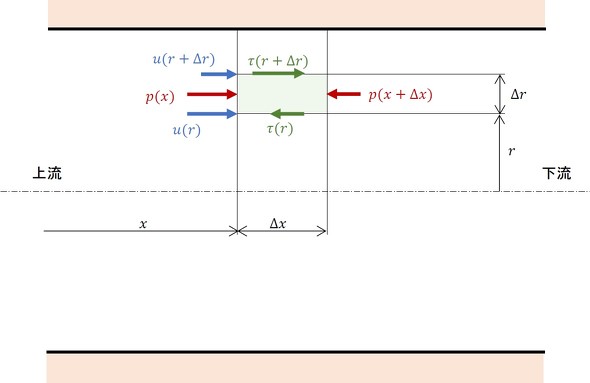
図5に微小円筒の断面を示します。半径rの位置における流速をu(r)、せん断応力をτ(r)、半径r+Δrの位置における流速をu(r+Δr)、せん断応力をτ(r+Δr)とします。流れの方向の位置をxとし、位置xにおける圧力をp(x)、位置x+Δxにおける圧力をp(x+Δx)と表します。また、圧力は半径方向には変化しないもの(一定値)とします。
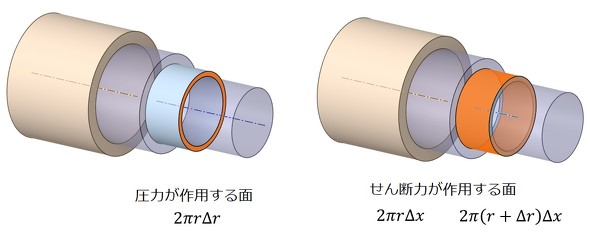
図6に圧力が作用する面と、せん断応力が作用する面の面積を示します。圧力×面積、せん断応力×面積が作用する力なので、微小円筒に作用する力の釣り合い式は、式3となります。
式3の青文字で書かれた部分は、せん断応力τがrやr+Δrの関数であることを示しています。一方、赤文字で記された(r+Δr)は、単に(r+Δr)を掛け算していることを意味します。
式1を代入します。
図6において「せん断応力の方向が反対ではないか?」とお気付きになるかもしれません。実際、流速はパイプ中心で最大値に、パイプ壁面ではゼロになるため、du/dr(※1)はマイナス値となります。よって、せん断応力は図示した方向とは反対向きに作用していることになります。
以前「頭にたたき込んでおいてください」と強調した式5を、式4に代入します。
計算を進めます。
Δのある項とない項があります。Δのある項は微小項であるため、これを無視して計算を進めます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

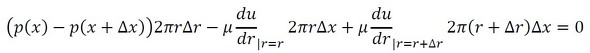
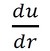
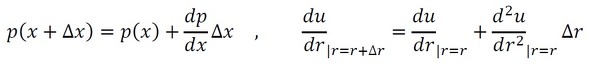 式5
式5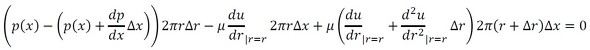
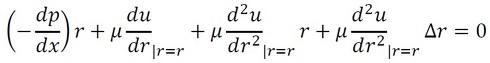 式7
式7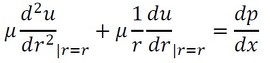 式8
式8





