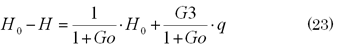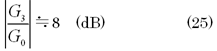ラプラス変換と割り切ったお付き合いをするよ:独学! 機械設計者のための自動制御入門(6)(3/4 ページ)
なお、Excelのエンジニアリング関数の中の「複素関数」(complex、imabs、imargumentなど)を使うと、複素数の演算は簡単にできます。
では、ラプラス変換を使って、図2のボード線図を描いてみましょう。
まず、浴槽の水位特性である伝達関数G3の浴槽の断面積Sを1m2とします。
すると、以下のようになります。
ゲイン|G3|は−20・LoG(ω) (dB)、位相遅れ∠G1はωに関係なく一定値のπ/2(rad)=90°ということが分かります。ボード線図のゲイン曲線は、横軸はLoG(ω)なので、1(rad/min)で0(dB)を通過する−20の直線となっていることに注意してください。
次に、バルブ流量特性の流量係数aを10(m3/min/m)とすると、
ゲイン|G2|は20・LoG(10)=20 (dB)、位相遅れ∠G2は0°です。いずれもωに無関係に一定な値です。
最後にバルブのモータコントローラの伝達関数G1ですが、積分だけの場合、積分要素の係数bを0.1(1/min)します。
ゲイン|G1|の曲線は20・LoG(0.1)−20・LoG(ω)=−20−20・LoG(ω) (dB)です。これはG3のゲイン曲線より−20(dB)小さい直線です。そして位相遅れ∠G3は、G3と同様、ωに関係なく一定値の90°です。
実は、図2はこのようにして計算されたものです。
第2回で、叔父さんは、周波数応答特性(ボード線図)は、実験によって得ることができるっていってたけど、ラプラス変換を使ったブロック線図からも計算できるんだね
実はそうなんや。浴槽の水位特性の周波数応答特性を実験で求めるとなると大袈裟(おおげさ)になるやろ? 浴槽の水位制御のような単純なシステムでは、実験するより計算で求める方がはるかに簡単やで。普通、制御システムを設計する場合には、システムの運動や状態についての運動方程式や状態方程式を立てて、それらをラプラス変換してボード線図を描くんやけど、いきなりラプラス変換は、ちょっと敷居が高いかな、と思ったんや。だから、初めは、ボード線図は実験でも求めることができるっていう説明をしたわけや
ふ〜ん。ラプラス変換も、計算ツールだと割り切って、いわれたとおりの方法に従って計算すれば、別に難しくないけどね
さよか。それなら、これからは、ラプラス変換を使うことにしようか
とにかく、僕の考えた積分制御では、システムが不安定となることが図2のボード線図から分かったし、いまの説明でそのボード線図がどうやって得られるかも分かったよ。次は、積分要素と比例要素を組み合わせて、どうやってシステムを安定化させるか、という番だね。具体的に、積分要素の係数bと比例要素の係数cの値を、どうやって決めるのさ?
その前に、比例制御だと、偏差hが0にならないので目標値に到達しないのが問題だ、ということだけど、その偏差がどのくらいなのか確認してみようや
まず、比例制御のブロック線図を描くと図6となる。
ここで、各伝達関数は、
G1=c
G2=a
だから、開ループシステムの伝達関数Goは……
叔父さんのいうとおり、s=iωとおいて、ωを0から+∞まで変化させてボード線図を描く。ここで、浴槽の断面積Sは1m2、バルブの流量特性aは10(m3/min/m)という値が設定されているけど、比例要素の係数cの値が決まっていない。cはいくつにすればいいかな?
cは、浴槽水位の目標値hoと現在の水位hとの差h(m)を、バルブの開度x(m)に変換する係数だ。例えば、偏差hが100mmのとき、バルブの開度xを4mmぐらいに開けるということにすれば、c=4/100=0.04だ
ちなみに前回、付録で紹介した浴槽水位のシミュレーションでは、最大給湯量qmaxを0.08(m3/min)としています。バルブ開度xでの給湯量はq=a・xですから、最大給湯量qmaxで給湯するためのバルブ開度は、バルブの流量特性a=10 (m3/min/m)のとき、x=q/a=0.08(m3/min)/10 (m3/min/m)=0.008 (m)=8 (mm)です。従って、偏差hが100(mm)のとき、バルブの開度xを4(mm)ぐらいに開けるという設定は、水位が目標値より200(mm)下がったときに、バルブを全開、あるいは、バルブの最大開度を8mmとする設定である、といえます。
するとボード線図は図7のようになる。今度は、位相余裕は90°あるね
開ループシステムに積分が1つしかないから位相遅れがせいぜい90°だ。従って安定限界である位相遅れ180°に対して90°の余裕がある。しかし、『だから、OK!』というわけではない
図6の比例制御は、図7のボード線図から位相余裕が90°もあるので安定であることが分かります。しかしいくら時間が経過しても、水位hは目標水位ho には到達しません。
前回(第5回)で説明したように水位hは、このようになります。
目標水位hoとの偏差は、
となります。
ところで、時間が十分経過したときの状態は、周波数応答で表現すると周波数ωが非常に小さいときの応答ということでした。そこで図7で、ω⇒0 のときの各伝達関数の応答を見ると、|Go|⇒∞、|G3|⇒∞ですから(23)式はω⇒0で、
となります。伝達関数G3とGoの割り算は、ボード線図上では引き算ですから、図7に示すように、ゲイン差は、
となっています。8(dB)を比に直すと10(8/20)≒2.5です。漏れ量qを最大給湯流量qmax=0.08(m3/min)の1/10の0.008(m3/min)とすると、
の偏差が発生することになります。
実際に、前回(第5回)と同様に、今回付録するExcelのシミュレーション(記事末参照)で確認すると、確かにそうなっているのが分かります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
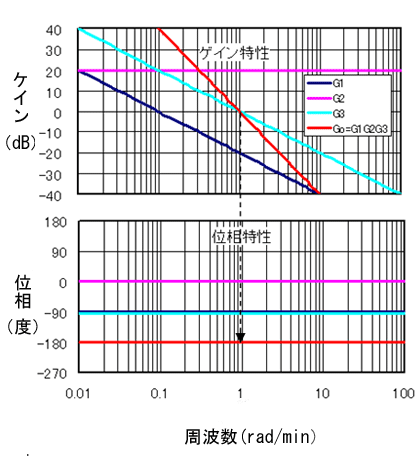 図2(再掲)
図2(再掲)

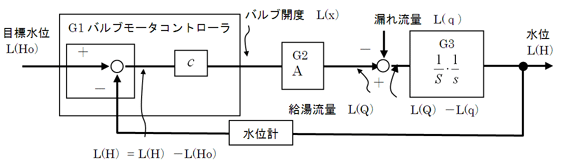 図6 比例制御による浴槽水位制御ブロック線図
図6 比例制御による浴槽水位制御ブロック線図 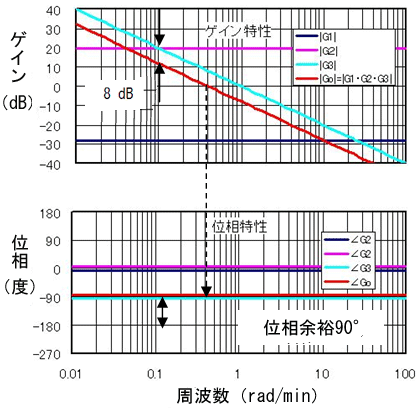 図7 図6の比例補償制御システムの各伝達関数のボード線図
図7 図6の比例補償制御システムの各伝達関数のボード線図