制御設計の基本! ボード線図を極めよ:独学! 機械設計者のための自動制御入門(9)(2/4 ページ)
この2つの伝達関数からなる掛け算とちゃうん?
そういわれればそうだね
確かに……
じゃあ次、PID制御にいこか
もう次にいっちゃうの!? PI制御のボード線図の話はまだ聞いてないよ
あとで、まとめて話すわ。勉強も料理と一緒で、下ごしらえが大事なんや。PID制御はどうなる?
関西人はせっかちだからいやなんだ……
なんやて? 叔父さんはれっきとした湘南ボーイやで。今年のノーベル化学賞もろた根岸博士は、叔父さんの中学、高校の先輩やで……どや、すごいやろ
なにがすごいの? おじさんがノーベル賞もらったんじゃないじゃん……
誰の近くにもすごい人がいるってことや。普段はそれに気が付かへんだけや。草太のお父さんだって、案外、本当はすごい人かも知れへんで
分かった、分かった……それで……PID制御の場合は図5に示すように、比例要素と積分要素と微分要素を並列に加算したものだから……
KDが微分要素の係数やな
さらに変形して
今度は分子がsの2次式となったよ
この2次式が因数分解されるとしようか、すると
ずいぶん都合のいい話だね。因数分解できるという保証はどこにもない
いいの、いいの。後で分かるから。ついでに、比例と微分からなるPD制御もやっておこうか。PD制御の場合は……
なんか分かってきたぞ。いずれも、比例値Kとラプラス演算子sの一次式(τ・s+1)と積分要素1/sの掛け算から構成されているんだ
ついでにいうと、ステアリングの伝達関数G2も実は、こう書ける
これについては、後でまた話す機会があるやろ。とにかく、伝達関数の基本形は、これに微分のsを含めて次の5つということが分かった。 K、s、1/s、1+τ・s、1/(1+τ・s) つまり多くの伝達関数はこれらの掛け算で表すことができるんや。実際の設計ではこれに『無駄時間遅れ 』やsの2次以上の高次の式も現れるけど、学習の基礎知識という意味ではこれくらいで十分と思うで
この5つの要素のボード線図が理解できれば、あとはそれらの足し算、引き算を使って求めることができるっていうこと? でも、ボード線図の足し算ってどういうことだっけ?
なんや、なんや。それでも大学院生かい。だから日本の科学技術のレベルが落ちてきたっていわれるんや
独り言だよ、独り言。ちょっといってみただけだよ
それなら、説明してみてや
ボード線図って横軸は周波数ωの対数表示だよね。そしてゲイン特性の縦軸は20・loG(|G|)でしょ。伝達関数G1の、あるωのゲインa=20・loG(|G1|)と、同じωの伝達関数G2のゲインb=20・loG(|G2|)を足し合わすっていうことは……、なんだ、G1とG2のゲインの差だけG1のグラフが上下するだけじゃん。つまりG1とG2のゲイン曲線を足し合わせると図6のようになるんだ。位相も同じだよ
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査



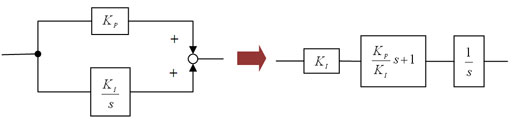 図4(再掲)
図4(再掲)

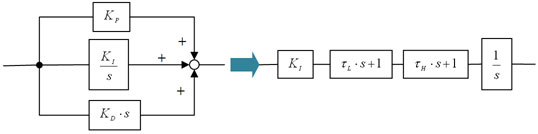 図5 PID制御のブロック線図
図5 PID制御のブロック線図 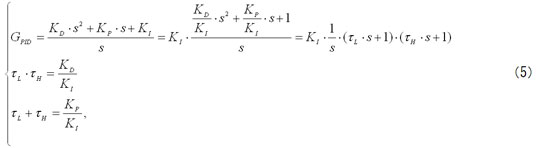
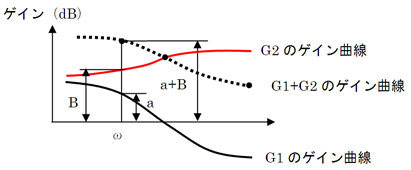 図6 ゲイン曲線の加算
図6 ゲイン曲線の加算 





