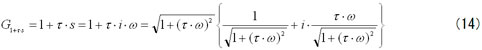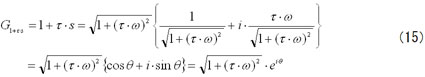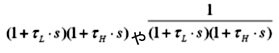制御設計の基本! ボード線図を極めよ:独学! 機械設計者のための自動制御入門(9)(3/4 ページ)
そういうことやな。じゃあ、さっきの5つの伝達関数のボード線図を詳しく調べてみようか。まず、比例要素についてや。伝達関数はGP=KPやな。KPは一定値や。さっき説明したけど、もう一度複素指数関数で表してみると
だから
このボード線図は図7のようになる。ゲイン、位相ともに周波数ωに関係なく一定値や。つまり横軸に平行な線やな
比例制御というのは、制御対象のゲイン特性を上下に移動させる働きがあるってことだね。だから、比例係数KPを大きく取り過ぎるとゲイン曲線が上に上がって位相余裕が小さくなり、システムが不安定になるんだね
そうや。次は微分要素Gs=sと積分要素G1/s=1/s。s=i・ωとおくと……
s=i・ωがようやく出できた……
微分要素は
積分要素は
だから微分のゲインと位相は
積分のゲインと位相は
微分と積分は正負が違うだけで、同じ形の式だね。ボード線図では横軸がlog(ω)だから、微分のゲイン特性は横軸に対して勾配20の登り直線になるんだね。積分は反対に勾配−20の降り直線になる。位相はともに周波数ωに無関係の値で、微分は90°(π/2)、積分は−90°(−π/2)。つまり、微分は位相が進んで、積分は位相が遅れる。これらの特性を、横軸にlog(ω)をとってグラフを書くとすれば図8のようになる
対数表示した周波数軸で、周波数が10倍になる区間をデカード(decade)と呼ぶんやけど、微分、積分要素は、1デカードあたり20(dB)それぞれ直線的に増加、減少するやろ。それで、微分要素、積分要素のゲイン特性はそれぞれ-20(dB/decade)、+20(dB/decade)の勾配を有する直線であると説明することがあるんや。知らなくてもかええけど、知っておいても損はないわ
あっそう
次は1+τ・sの伝達関数のボード線図や。ちなみに1+τ・sを『一次進み要素』というんやで。なぜ進み要素と呼ぶかは、ボード線図を描いてみれば分かると思うで
分かった。今度は僕が計算するよ
ここから先が問題だね……
おっ、いいぞ。まんがれ!
まんがれ。……久々に出たね。それはともかく……
ゲイン20・log(|G1+τ・s|)は
そして位相は
だから
つまり一次進み要素1+τ・sのゲインと位相は……
これを、ωを、例えば0.01(rad/s)から100(rad/s)までエクセルで計算すればボード線図が描けるね
うん。ええな。確かに実際の計算はエクセルでやるんやけど、1+τ・sのボード線図の特徴を知っておくと実際の制御設計に非常に役立つで
えっ、どういうこと?
つまりやな。いちいちエクセルで計算しなくても、τが分かればすぐ1+τ・sのボード線図を描くことができるんや。1+τ・sのボード線図が描ければ、その積……
……のボード線図も簡単に描けるわけや。反対にボード線図から、その伝達関数の構成を推定したり、τの値を推定できることもあるわけや
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞




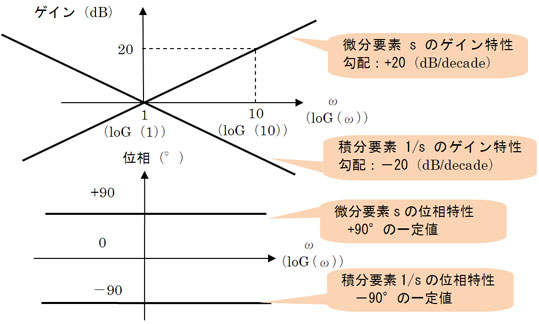 図8 積分(I)要素と微分(D)要素のボード線図
図8 積分(I)要素と微分(D)要素のボード線図