これで完全マスター! PID制御:独学! 機械設計者のための自動制御入門(10)(1/3 ページ)
今回は、いよいよPID制御のまとめ。ボード線図を使いつつ、シミュレーションもしながら、動特性を改善していこう
当連載の登場人物
銀二(ぎんじ)
設計コンサルタント。甥(おい)っ子の草太を自分の息子のようにかわいがっています。
草太(そうた)
銀二の甥。現在は大学院生です。ちょっと困るとすぐ叔父を頼ってしまうちゃっかり者だけど、頑張り屋さんです。
今回は、いよいよPID制御のまとめです。PI制御にD制御を加えたPID制御の設計を、前回復習したボード線図を使って行い、シミュレーションによりいかに動特性が改善されるか確認し、ボード線図を使った設計がいかに有効か、確かめていきましょう。
草太、再び明石へ
東京在住の草太ですが、瀬戸内海の風香る、銀二さんの書斎へまた戻ってきました。
叔父さん、ただいま。
なんや、また来たんかい。
いやー。この辺の気候が気に入っちゃってさぁ。また来ちゃったよ。
また来ちゃった、じゃあらへんがな。お母さん、怒っとんとちゃうんかい?
もう子どもじゃないんだから、いちいち親の指図は受けないよ。ここまで来たら、PID制御を完全にマスターするまでは帰らないことにしたよ。
そうか、じゃあ今回でPID制御を完璧にマスターしてもらおうか。まず前回やり残したPID制御のコントローラーのボード線図を簡易作図法で描いたらどうなるかってところから始めようか。
叔父さん、家で復習してきたから僕が描いてみるよ。
そうか。それならやってみ。
比例要素の係数をKp、積分要素の係数をKI、微分要素の係数をKDとすれば、PID制御の伝達関数GPIDは……。
前回、叔父さんは、これが因数分解できると仮定したよね。すると、こうなる。
よう覚えとんなぁ。
家に帰ってから、復習したからね。ボード線図については、もうバッチリ理解したよ。
(2)式右辺の始めの項を見るとKIだね。KIは、全体に掛かる比例係数だから、ゲイン曲線を上下させる機能がある。KIを大きく取ると位相余裕が小さくなって不安定になる。つまり、応答が振動的になるんだ。反対に小さく取ると安定化する。だからKIは位相余裕やゲイン余裕を見ながら最後に決めればいいと思うんだ。だからここではKI=1として話を進めるよ。
いい線いってるで……。
ほんと? でもKPではなくKIに比例的機能があるというのは不思議な感じがするね。
ほんまやな。それはPID制御が並列制御やからや……。
そういうことか……。次に(2)式右辺の2つ目は積分1/sだね。ボード線図は、位相曲線が−90(°)の水平直線で、ゲイン曲線はω=1(rad/s)のとき0(dB)の点を通過する−20(dB/decade)の直線だね。これは1(rad/s)以下の周波数ではゲインを増やし、1(rad/s)以上の周波数でゲインを下げる機能がある。
ええぞ、ええぞ。
で、(2)式右辺の(τL・s+1)(τH・s+1)のボード線図は、τL・s+1とτH・s+1の掛け算だけど、ボード線図上では足し算になる。
一次進み要素のボード線図は前回学んだよな。
一次進み要素τ・s+1の位相曲線は、ω=1/τのとき位相45°を通るS字曲線だ。ゲイン曲線はω=1/τで0(dB)を通って、それ以降は20(dB/decade)で上昇する折れ線。本当はω=1/τで3(dB)を通るんだけど簡易作図だからそれでいいんだ。すると2つの一次進み要素のボード線図はそれぞれ図1の黒やブルーのグラフのようになる。
τL>τHとするとωL=1/τL<ωH=1/τHや。τは時定数って呼ばれている。
τL>τHって変な感じがするけど、その逆数の周波数に意味があるんだね……。それで……、2つの一次進み要素の積(τL・s+1)・(τH・s+1)のボード線図は、それらのボード線図を足し合わせたものだから図2の赤の曲線となる。
この赤の曲線に積分1/sのゲイン曲線を足し合わすとゲイン曲線を回転させることができる。
ゲイン曲線を回転?
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞








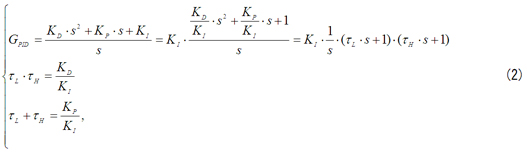
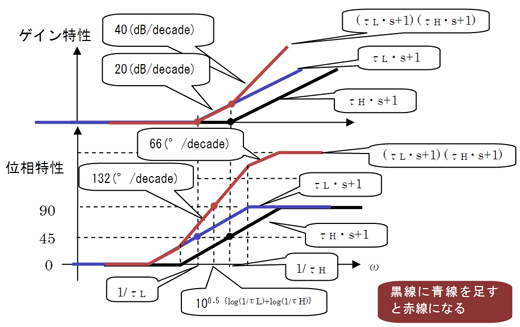 図1 2つの一次進み要素のボード線図
図1 2つの一次進み要素のボード線図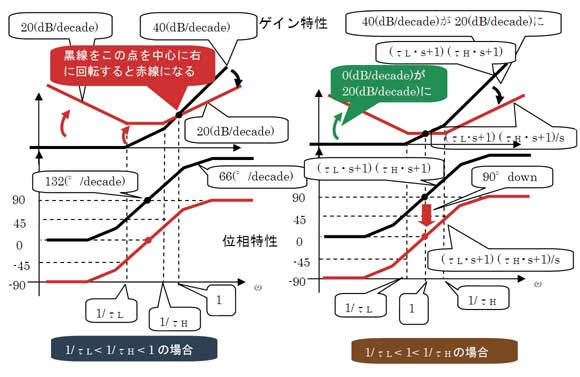
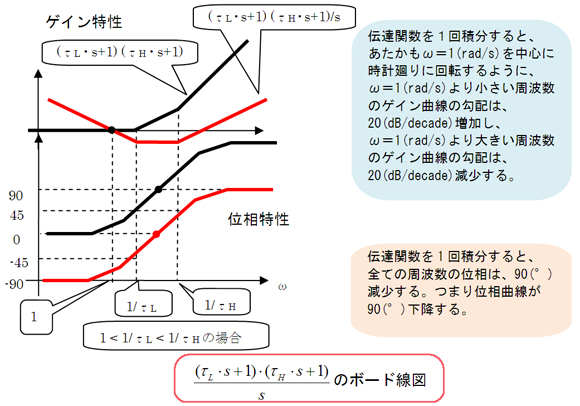 図2 ボード線図を足し合わせると?
図2 ボード線図を足し合わせると?





