現象のモデリングの勘所 〜現象の式のマトリクス表現〜:1Dモデリングの勘所(43)(1/3 ページ)
「1Dモデリング」に関する連載。連載第43回では「現象のモデリングの勘所」をテーマに取り上げる。
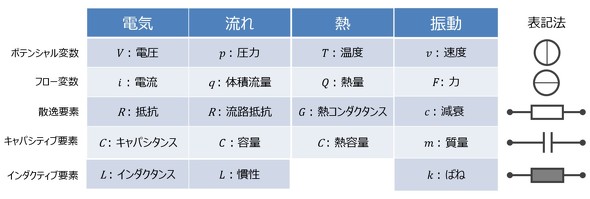
まず、現象のモデリングについておさらいしたい。現象のモデリングは、基本的に状態変数のフローを追いながら(電気回路を描くように)フロー図を作成し、この図に基づいて電流則と電圧則(キルヒホッフの法則)を用いて式を導出し、解くという手順で行われる。
この手法自体に何ら問題はない。だが、図を描いた段階では視覚的に理解できるものの、式になると(これは式表現の宿命ではあるが)変数間の関係が分かりにくくなる。これは、式の中で独立変数と従属変数が明確でないことに起因している。そこで今回は、現象の式をマトリクス表現にすることで、この問題の改善を試みる。
ドライヤーのモデリングの振り返り(参考文献[1])
図1の現象の共通表現用法を用いて、フロー図の作成と定式化を行った。
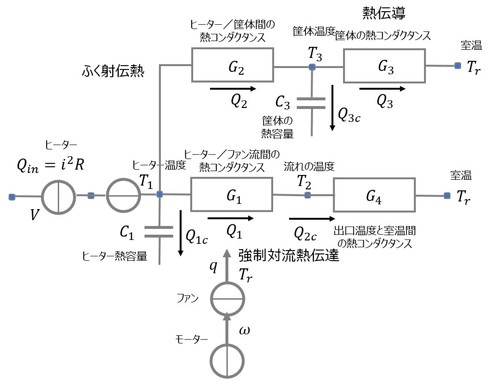
図1に従って、ドライヤーのモデリングを行う。図2に、ドライヤーのフロー図を示す。
この図では、ジュール熱Qinの流入を起点として、ドライヤー各部への熱の流れを表しており、それぞれの温度(ヒーター、出口流れ、筐体)を求めている。流れ自体はその流量を外部(電気、モーター、ファンの連成解析)で求め、ヒーターの入り口に入力している。つまり、流れの入り口温度はTrで、出口温度はT2である。これを踏まえると、
となる。q、ρ、cはそれぞれ、空気の風量、密度、比熱である。同様に、
となる。このあたりの説明は、前回の内容では不十分であった。
図2を基に定式化すると以下となる。
熱の流れの連続性(電流則)から、
が成り立つ。各要素の熱コンダクタンスに関しては、
となる。さらに、ヒーターの熱容量C1[J/K]、出口温度と室温間の熱コンダクタンスG4[W/K]、筐体の熱容量C3[J/K]に関しては、
となる。これらを用いれば各部の温度、熱量が求まる。このとき、独立変数はQin、T1、T2、T3のみであり、他の変数は全て従属変数である。このことは上式からも、図2からも分かりにくい。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- キヤノン社員が技能五輪国際大会の工業デザイン技術職種で日本代表に
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
 式4
式4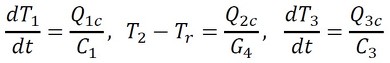 式5
式5





