これで完全マスター! PID制御:独学! 機械設計者のための自動制御入門(10)(2/3 ページ)
回転するって言ったのはおまえだぜ。前回そう言ったやろ? 覚えてへんか? 正確には回転とは違うけど、ゲイン曲線は、図1の(τL・s+1)・(τH・s+1)の赤い曲線とω=1(rad/s)の交点を中心として、あたかも右回転するように変形するんや。図2を見れば理解できるやろ。
なるほどね。図2の1/τH<1、1/τL<1<1/τH、1<1/τLのときのグラフをみるとよく分かるね。積分1/sがゲイン曲線を時計回りに回転させるような効果があるねということは、微分sは反時計回りに回転させるような効果があるんだ。
そういうこっちゃ。だから、制御系に積分補償を加えると、低周波域のゲインがω→0で、∞となる。その結果、静特性が改善される。一方微分補償を加えると高周波域でのゲインがω→∞で∞となる。その結果、第8回で学んだようにカットオフ周波数が高くなり応答性が改善されるわけだ。しかし、積分補償の場合は位相が90°下がるから位相余裕がなくなるというデメリットがあるし、微分補償の場合は、高周波数ほどゲインが大きくなるので雑音を過剰に増幅してしまうというデメリットがある。
分かってきたぞ。PID制御をすると、低周波域と高周波域の両方でゲインが増加するから、静特性と動特性のいずれも改善することが期待できるんだ。
簡単に言ってしまえばそういうことなんや。よっしゃ、これでPID制御補償のコントローラーG1のボード線図がどういうグラフになって、どういう機能があるか分かったやろ。
ついでにPD制御とPI制御について考えてみると……。
だから、それぞれのコントローラーのボード線図を描くと図3、図4のようになるね。
いよいよPID制御の実践だ!
それじゃあ、横風を受けるときの自動走行制御システムにPID制御をすると、開ループ伝達関数Goのボード線図がどうなるか調べようか。まず、基本に立ち返って第9回の図3のブロック線図を思い出してみようや。
横風を受けるときの自動走行制御システムのブロック線図だね。車体が横風を受けてδ°旋回するから、風がなければ反対方向にδ°旋回するようにハンドル操作してやれば、相殺されて車は真っすぐ進む。そういう制御を車体の向きを検知して自動的にやろうということだね。
フィードバックシステムで重要なのは開ループの伝達特性における位相余裕あるいはゲイン余裕の大きさやったな。開ループの伝達関数はGsとG1とG2の掛け算や。コントローラーG1の伝達関数はGP、GPI、GPDあるいはGPIDのどれにするか最初は決まってへん。だから、まずはG1を除いたステアリングG2と車体Gsのボード線図を合体させる。すると図5のようになる。
第9回の図3のG1とG2のボード線図を合体させて1つの伝達関数としてみるんだね。
「真ん中のブロックG1を無視して、離れた2つのブロックを合体させていいの?」と思う人は、直列にならんだ3個の乾電池の順番入れ替えても同じや、と考えればいい。その説明で満足しない人は、線形理論を前提とした制御理論だから、と言えば分かるやろ。
ステアリングの伝達特性G2は、第3回の図9に示した方法で実験的に求めたんだよね。
ステアリングの具体的なボード線図は第4回の図2で紹介しました。車体の伝達関数については第4回の図3にその考え方を示し、図5に計算した結果のボード線図を載せています。
よく覚えとったなぁ。時速40kmで走っている車体のタイヤが1(rad)曲がると1秒あたりでは進行方向と垂直な方向、つまり横方向に40(km/h)×1000/3600(h/s)=11.11(m/s)の速度で移動するから、1°では11.111/180×π=0.194(m/s)の速度で移動する。横方向の移動距離は運転している時間だけ変化するから、これを積分したのが車体の伝達関数Gsとなる。ラプラス変換表示すれば、
Gs=0.194/s (5)
や。
ステアリングG2のボード線図は実験で求めたんじゃないの?
第4回でも言ったことやけど、ステアリングの周波数応答特性は実験でも求められるが、計算からも求めることができる。これについては、またあとで詳しく説明するとして、取りあえずステアリングG2の伝達関数は(6)で与えられると思ってや。あるいは第4回の図2のボード線図から(6)を推定したと思ってもらってもええで。
図7のGs・G2のボード線図に図2のコントローラーG1=GPIDのボード線図を足せば、開ループ伝達関数のボード線図が得られる。
位相余裕が大きく、かつカットオフ周波数が高くなるように(1)のKP,KI,KDを選択すればいいんだよね。
そうやけど、図2のコントローラーG1=GPIDのボード線図は、KP,KI,KDの値が決まってないと描けへん。だから、まずは、適当にKP,KI,KDの値を決めてやって、G1=GPIDのボード線図を描く。そして、図7のGs・G2のボード線図とを足して、開ループの伝達関数Go=G1・Gs・G2のボード線図を描くんや。
すると、KP,KI,KDの値は試行錯誤で決めるっていうこと? そうじゃなくて、もっと合理的な方法で選択する方法はないのかな?
そうやな……。実際の設計ではボード線図はエクセルやその他制御設計用の専用ソフトを利用するから、KP、KI、KDをいろいろ変えてボード線図を描くことは簡単にできる。そうやってボード線図を描いてみると、KP、KI、KDの値によってグラフがどう変わるか、その傾向が見えてくる。だから、草太が思うほど面倒やないんやで……。あえて、というなら、こんな方法はどうやろ。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査



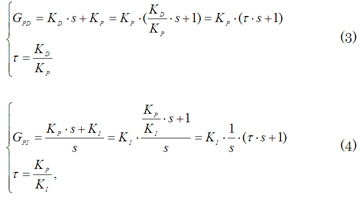
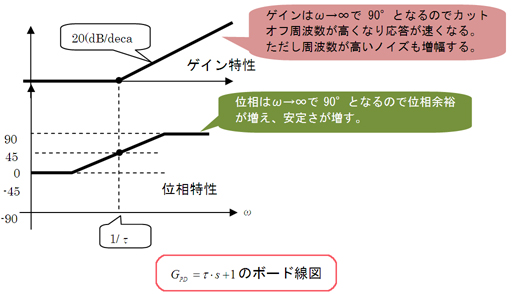 図3 PD制御のボード線図
図3 PD制御のボード線図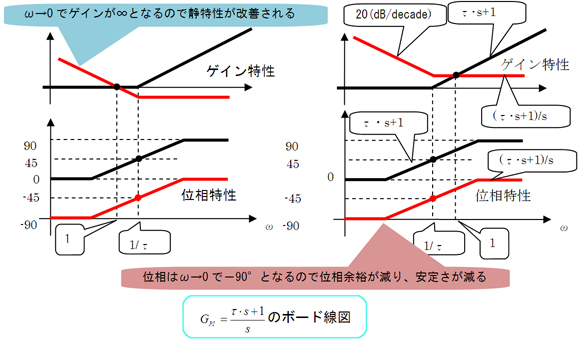 図4 PI制御のボード線図
図4 PI制御のボード線図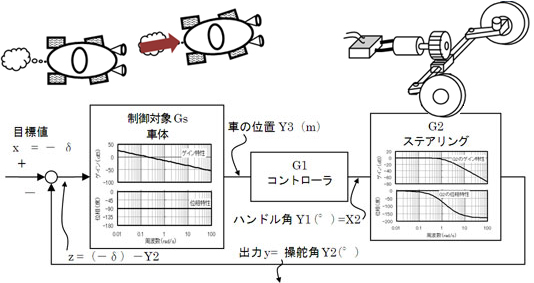 第9回の図3 横風を受けるときの自動走行制御システムの構成
第9回の図3 横風を受けるときの自動走行制御システムの構成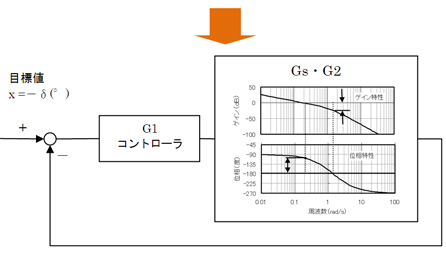 図5 横風を受けるときの自動走行制御システムの構成(今回)
図5 横風を受けるときの自動走行制御システムの構成(今回)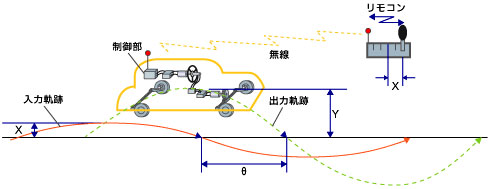 第3回の図9 自動車運転用実験者の周波数応答特性計測
第3回の図9 自動車運転用実験者の周波数応答特性計測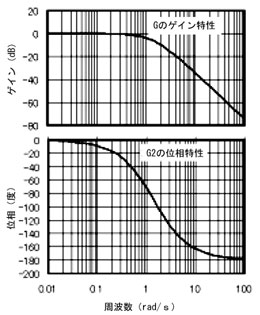 第4回の図2 操作部G2のボード線図
第4回の図2 操作部G2のボード線図 図6 タイヤのステアリング角度が1°のときの車の横方向移動速度
図6 タイヤのステアリング角度が1°のときの車の横方向移動速度
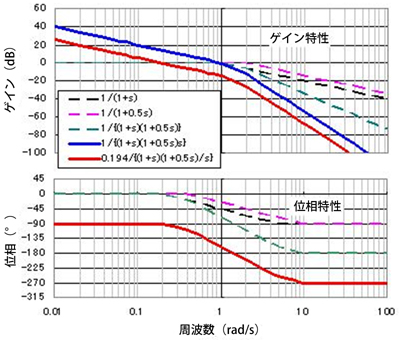 図7 GsとG2が合体したボード線図(簡易作図)
図7 GsとG2が合体したボード線図(簡易作図)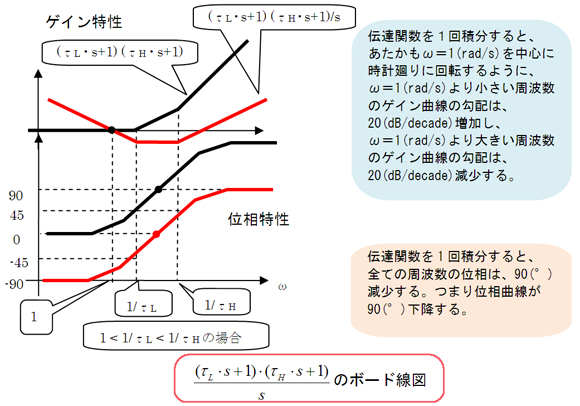 図2
図2 式1
式1





