これで完全マスター! PID制御:独学! 機械設計者のための自動制御入門(10)(3/3 ページ)
補償制御の本質が見えてきた
銀二さんは、次のような方法を説明し始めました。
図3のコントローラーG1をPID制御としたときの各ブロックを伝達関数で表示すれば、図8のようになります。
この制御ブロック線図を見て、何か思わへんか?
コントローラーG1の位相進みとGs・G2の位相遅れの2つの位相曲線は周波数軸に対して対称だから、それらを足し合わせたときの位相は互いに打ち消しあって0や。それで、2階積分による位相遅れ180°が残ってしまう。ならば、制御対象G2・Gsの2つの一次遅れ要素のうち、どちらかを消す、というのはどうや? そうすれば位相遅れは180°より少なくなるやろ?
その場合、1/(1+0.5・s)と1/(1+s)のどっちを残すようにすればいいんだろう?
当然1/(1+0.5・s)や。
どうして?
応答性はカットオフ周波数の高さで決まるからや。
制御対象の特性を、1/(1+s)とするより1/(1+0.5・s)とした方が、システムの応答性は高くなるというわけです。従って、図8は図10に、さらに図11のようになります。
草太は、図11の制御ブロック中の伝達関数の時定数τが、0.5(sec)より大きいときと、小さいときの2つのパターンに分けてボード線図を描きました(図12)。
図14を見るとτが大きいほど低周波数のゲイン曲線の持ち上がり方が小さく、τが小さいほど低周波数のゲイン曲線の持ち上がり方が大きいことが分かります。つまりτが大きいほど静特性がよくないことになるわけです。ですから必ずしもτが大きければいいということにはなりません。
なるほどね。τを大きく取ると、安定性は確保できるけど、静特性が確保できない。反対に、τを小さく取ると、静特性は確保できても安定性が確保できない、ということなんだ。
 (式2)
(式2)
KIはどうやって選ぶの?
KIは、図14のゲイン曲線を上下に動かす機能があるから、望みの位相余裕とカットオフ周波数、つまり応答性が得られるようにKIを決める。
サーボ機構の場合、開ループシステムの位相余裕が40〜60(°)となるようにゲインを決めると、安定性と応答性がバランスよく確保できると、第3回でいってたね。
そうや。よく覚えていたな。ところで図14の3つのゲイン曲線が重なる高周波数域で特性は、何の特性やと思う?
大正解や! もう、草太には教えること、あらへん。
どうやら、草太はPID制御を理解したようです。しかし、現実のシステムには、非線形要素があります。従って、ボード線図から設定したKP,KI,KDの値で制御すれば必ず思ったような結果がでるとは限りません。そこで、実際の応答が満足いくようなものではなかったときは、KP,KI,KDの値を少し変えて応答を調べ、満足結果が出るまで最適な値を探索する、いわゆる「チューニング」を行います。その場合でも、位相余裕、ゲイン余裕、カットオフ周波数についての知識は、有能なナビゲーターとして設計者を助けてくれるでしょう。
なお、最近はシミュレーション技術が発達しているので、まずシミュレーションによる仮想実験で各制御パラメータの最適値の範囲を絞り込み、その後現物で微調整をするという方法が主流です。
ボード線図によるパラメータの絞り込みも、パラメータの値さえ入れてやればコンピュータが計算して描いてくれるのでそんなに大変なことではありません。しかし、その場合でも、制御の理屈を知ってパラメータを決めるのと、試行錯誤で決めるのでは、設計品質という意味では雲泥の差があります。
たとえ結果が同じでも、理屈に裏付けられた設計と、偶然得られた設計では、設計の質が違うってことだね。何か分かる気がする。同じお金でも、宝くじで得たお金と、働いた得たお金ではその重みが違うもんね。
ま、そういうこっちゃな。
図15は、τ=5、KI=2として、KD=10,KP=12としたときのPID制御の開ループ伝達関数のボード線図です。
比較のため、第8回の図4に示したPI制御の開ループ伝達関数のボード線図を一緒に載せています。位相余裕は両方共に、50(°)程度ですが、PID制御ではカットオフ周波数が0.35(rad/s)から1.5(rad/s)に高くなり、ゲインも20(dB)以上増加しています。つまり安定性を確保したまま、静特性、動特性を改善することができたわけですね。
以下の動画は、走行中に、突然横風を受けたときの車の軌跡をシミュレーションしたものです。自動走行制御システムとしてPI制御とPID制御を採用したときの、特性の差がよく表れていますね。
以上でボード線図を利用した制御設計の方法の基本的な説明は終わりです。
ところで、自動走行制御システムに要求される機能は、強風の中を真っすぐ走行させることだけではありません。車線変更や交差点での右折、左折もあります。次回は、車線変更性能において、車が車線変更するときの応答性が、図15のPI制御とPID制御でどのように違うか、シミュレーションによって確認した結果を紹介します。また車のステアリング特性の伝達関数G2が、どのようにして(3)式で表されるようになったかを併せて説明します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
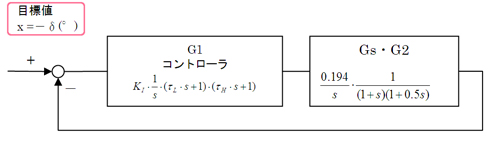 図8 横風を受けるときの自動走行制御システムの構成
図8 横風を受けるときの自動走行制御システムの構成

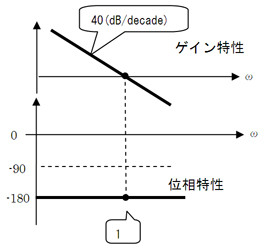 図9 ボード線図
図9 ボード線図

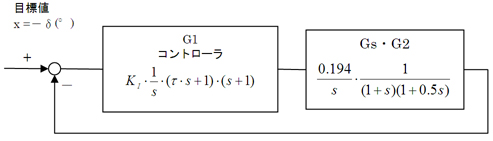 図10 横風を受けるときの自動走行制御システムの構成 1
図10 横風を受けるときの自動走行制御システムの構成 1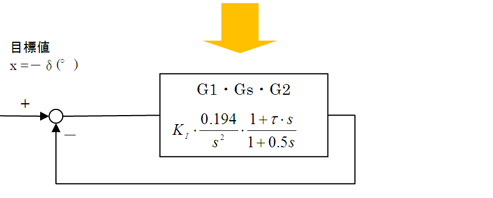 図11 横風を受けるときの自動走行制御システムの構成 2
図11 横風を受けるときの自動走行制御システムの構成 2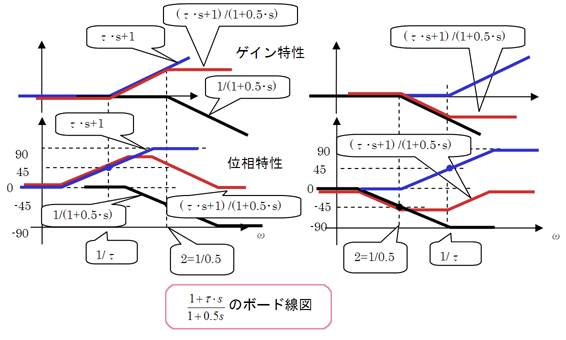 図12 ボード線図
図12 ボード線図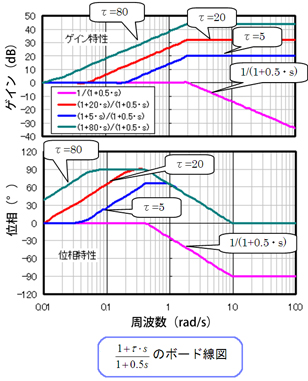 図13 ボード線図
図13 ボード線図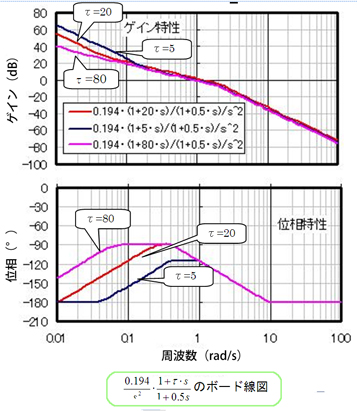 図14 ボード線図
図14 ボード線図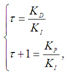

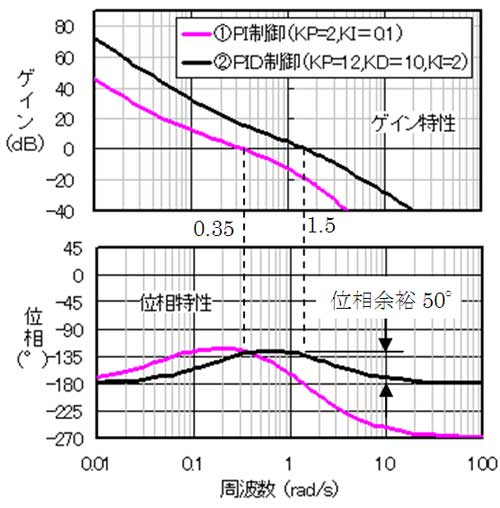 図15 PI制御とPID制御のボード線図
図15 PI制御とPID制御のボード線図






