「ふく射」による熱の伝わり:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(7)(1/9 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第7回は、「ふく射」による熱の伝わりについて考える。
今回は「ふく射」による熱の伝わりについてです。天気予報でよく耳にする「放射冷却の影響で、明日の朝は冷え込むでしょう」といっている“放射”のことです。
ここでは、温度の単位として「絶対温度(ケルビン[K])」が登場します。ちなみに、宇宙の温度は約2.7[K]、地表の温度は300[K]くらいなので、「温度差が大きいから熱が伝わる……」という表現は正確ではありません。
それよりも、地表から出ていくふく射熱は300の4乗(約81億)に比例し、宇宙からやって来る熱は2.7の4乗(約53)に比例するので、「地表から出ていく熱が圧倒的に大きいので朝冷える」という表現の方が正確です。
でも、曇りの夜は少し事情が異なります。雲の温度がだいたい280[K]くらいあるので、雲から地表に来る熱もかなり大きくなります。だから、そこまで寒い朝にはならないのだと思います。
ステファン・ボルツマンの法則のおさらい
さて、冒頭部分は読者の皆さんもよくご存じの内容だと思いますので、ふく射のおさらいとなります。
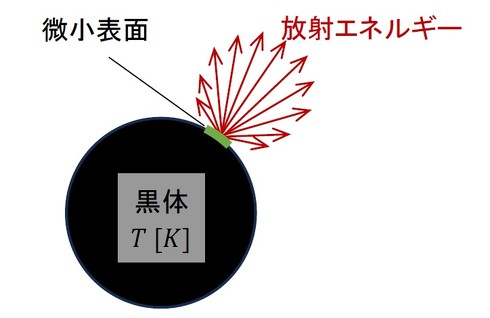
「黒体」とは、Wikipediaによると「外部から入射する電磁波を、あらゆる波長にわたって完全に吸収し、また熱放射できる想像上の物体」とされています。太陽の見た目は黒くないですが、黒体だと本で読んだことがあります。
図1は、黒体の微小表面から放射されるエネルギーについて示しています。
放射されるエネルギーを微小表面の面積で割った値qは、式1で求めることができ、これを「ステファン・ボルツマンの法則(Stefan-Boltzmann's law)」といいます。このときの比例定数σがステファン・ボルツマン係数で、その値は5.6687×10-8[W/m2K4]となります。
次に、「灰色体」という考え方を導入します。実在する物体の放射エネルギーは式1による値よりも小さくなります。そして、放射エネルギーは電磁波の波長により異なった値を取りますが、波長によらず一定とすると、放射エネルギーは式2で近似できます。
以前のシリーズ(連載「CAEと計測技術を使った振動・騒音対策」の第17回)で図2を掲載しました。
これと同じ式が成立します。式3です。
ここで大切な関係式があります。吸収された放射エネルギーは全部放射エネルギーとして放出されると考え、次式が成立します(式4)。
真空チャンバーなどを考慮すると透過するエネルギーはないので、「透過はない」として、t=0[-]で話を進めます。式5が成立します。
式5から分かるのは、反射率ρが1[-]であれば、放射率εはゼロになるということです。つまり、反射率が1[-]に近いシートで身体を覆えば、身体から放射される熱はゼロということになります。
ただ、震災時に、社員全員が体育館に集められ、銀色のシートが配布されて一夜を過ごしたことがありましたが、正直、それほど寒さを防げたとは感じませんでした。
その理由を考えてみると、人間の体温は309[K]くらいで、放射エネルギーは約517[W/m2]になります。仮に体温が300℃だった場合、放射エネルギーは約6110[W/m2]にもなり、10倍以上の差になります。
つまり、配布された銀色のシートは理にかなってはいますが、人間の体温レベルではふく射熱そのものがあまり大きくないため、実際には寒さをしのぐほどの効果は感じにくい、ということのようです。むしろ、熱伝達などの他の要因の方が影響が大きいのだと思います。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

 式2
式2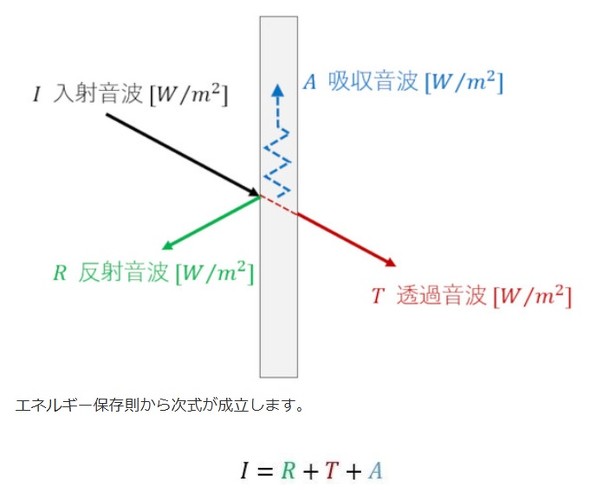
 式3
式3 式4
式4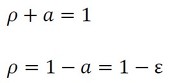 式5
式5





