「ふく射」による熱の伝わり:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(7)(2/9 ページ)
» 2025年05月12日 11時00分 公開
[高橋良一/RTデザインラボ 代表,MONOist]
練習問題をやってみよう
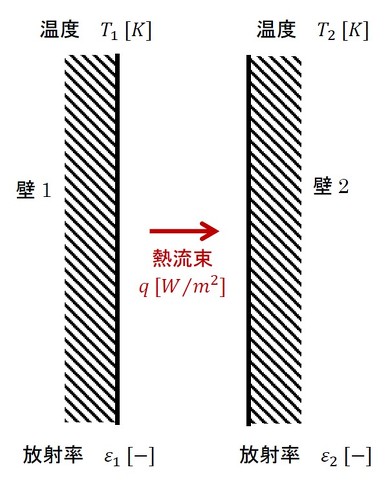
ふく射に対する理解を深めるために、練習問題に挑戦してみましょう。日本機械学会が主催している「計算力学技術者1級」の試験問題です。図3に示すように、とても近接した非常に広い壁があり、温度と放射率が与えられています。左側の壁の温度が高いときに、左側の壁1から右側の壁2に伝わる熱流束を求めましょう。もちろん真空中での問題です。
壁1の単位面積当たりの熱放射量E1は、式2から次式で表されます(式6)。
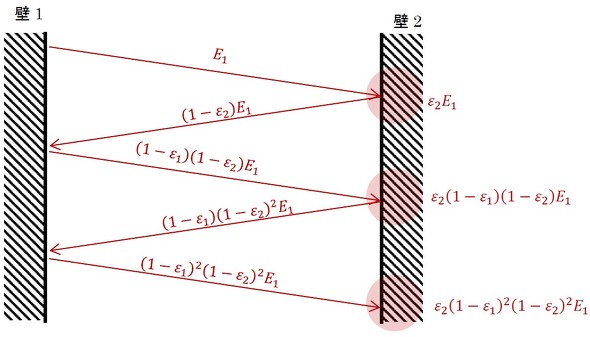
上記E1の全てが壁2に到着するとします。図4に示すように、E1は壁2が吸収する熱量(単位面積当たりです)と、反射する熱量に分かれます。
それぞれ以下となります。
壁2で反射する熱量の全てが壁1に到着する場合、それは壁1が吸収する熱量と、反射する熱量に分かれます。それぞれ以下となります。
壁1で反射する熱量の全てが壁2に到着するとします。図4に示すように、それは壁2が吸収する熱量と、反射する熱量に分かれます。それぞれ以下となります。
現時点での壁2が受け取る熱量は式7と式9の和ですが、図4から、壁2が受け取る熱量Q2は式10となります。
式10は、初項ε2E1、項比(1−ε1)(1−ε2)E1の等比級数の和なので、総和は次式となります(式11)。
同じ考え方で、壁1が吸収する熱量は式12となります。
壁1から壁2に伝わる熱流束(単位面積当たりの熱量)は以下となります。
E1、E2は次式でした(式14)。
上式を式13に代入します(式15)。
こんな感じでしょうか。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
Special SitePR
あなたにおすすめの記事PR

 式7
式7 式8
式8 式9
式9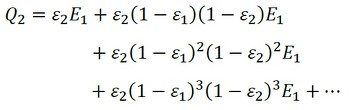 式10
式10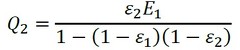 式11
式11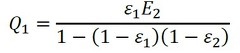 式12
式12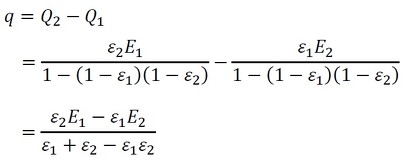 式13
式13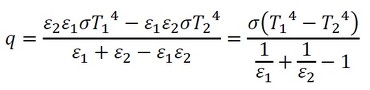 式15
式15





