「ふく射」による熱の伝わり:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(7)(3/9 ページ)
2つの黒体面間の熱のやりとり
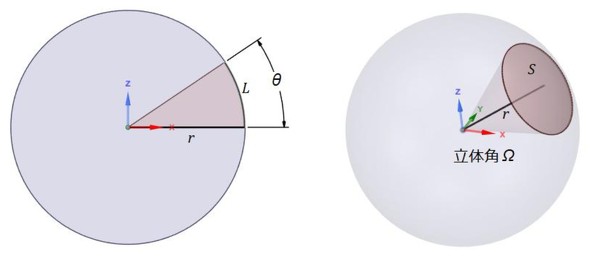
先に「立体角」について説明します。図5左図において角度θをラジアンで表すと式16となります。半径に角度を掛けると弧長Lが求まります。
図5右図において、立体角Ωは次式で定義されます(式17)。Sは面積です。
ここから小さな面が見えているとします。小さな面の立体角との距離が分かれば小さな面の見掛けの面積が求まります。
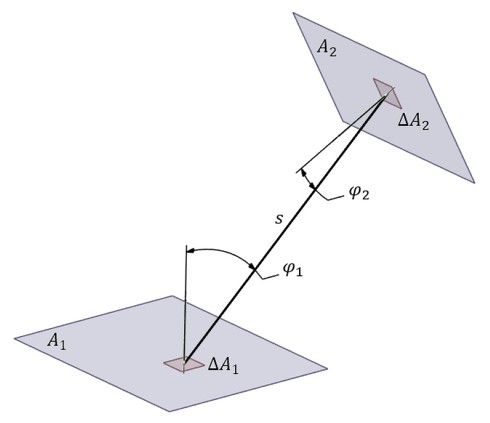
図6に2つの黒体面間の熱のやりとりを示します。微小な面ΔA1とΔA2とを結ぶ線を引きます。この線とΔA1の法線とのなす角をφ1、そしてこの線とΔA2の法線とのなす角をφ2とします。
今、放射強度Iという量を使います。面が表側の周囲に放射する単位面積、単位立体角当たりのエネルギーです。単位は[W/m2.sr]です。ΔA1からΔA2に単位時間当たりに放射されるエネルギーは式18で表されます。
ΔA1からΔA2に放射されるエネルギーは、I1ΔA1ΔΩ1でよいかと思われますが、cosφ1が付くのが「ランバートの余弦法則(Lambert cosine law)」です(参考文献[1])。このcosは放つ側のcosです。
立体角の定義からΔΩ1は式19で表されます。このcosはΔA2が傾いているためです。sは2つの面間の距離です。
式19を式18に代入します(式20)。
ΔA2からΔA1に単位時間当たりに放射されるエネルギーは、式21で表されます。
ΔA1からΔA2に単位時間当たりに伝わるエネルギーは、次式となります(式22)。
放射強度と温度は次式の関係があります(式23)。
式22を式23に代入し、積分すれば、A1面からA2面に単位時間当たりに伝わるエネルギーとなります(式24)。
T1、T2が一定温度の場合、式24のσ(T14−T24)を積分の前に出せます(式25)。
式25の積分は、A1面とA2面の位置関係だけで決まります。今、形態係数F12を導入すると、式25の積分は次式のように表すことができます(式26)。
形態係数F21を導入しましょう。対称性から式27が成立します。
A1面からA2面に単位時間当たりに伝わるエネルギーは次式となります(式28)。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン社員が技能五輪国際大会の工業デザイン技術職種で日本代表に

 式18
式18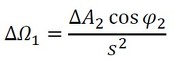 式19
式19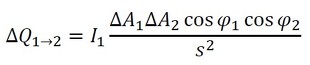 式20
式20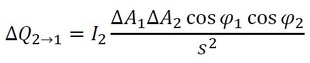 式21
式21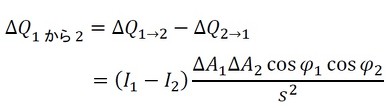 式22
式22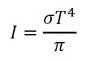 式23
式23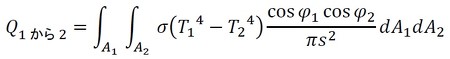 式24
式24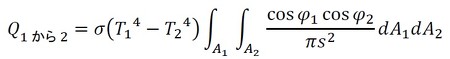 式25
式25 式26
式26





