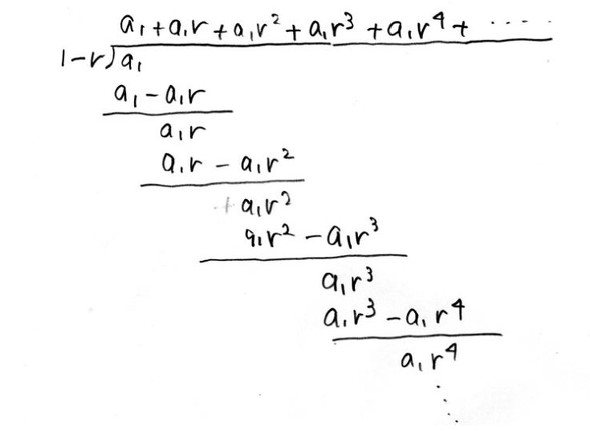「ふく射」による熱の伝わり:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(7)(7/9 ページ)
ランバート則は正しいのか
当然のことのように「ランバート則」が使われています。ここで、式18に注目します。式中のcosφ1は電磁波が出る側のcosです。今回、ふく射による電磁波と、反射による電磁波を検討しました。いずれもランバート則が適用されています。
ここでは電磁波(光です)の反射について述べます。反射にランバート則、つまりcosを掛けてよいのかを検討します。ランバート則を光の反射に適用すると、陰影のある表現が可能です。例えば、図15のような球の画像です。陰影から球体と分かります。
コンピュータグラフィックスの世界では「Torrance Sparrow則」(参考文献[3])を使うと、よりリアルな表現ができると“かつて”いわれていました。Torrance Sparrow則とは一言でいうと、「cosを掛けるのではなく、1に近い値を掛けると実験値と合う」というものです。cosを掛けない球の画像を図16に示します。
では、実際の月の写真と比較します。図17に示します。筆者にはcosなしの画像の方が実際の月に近いように見えます。特に、エッジ部に注目するとランバート則では暗くなっていますが、実際の月のエッジ部は全然暗くないのです。つまり、光(電磁波)の反射ではランバート則を適用できないと思っています。ふく射は赤外線なので電磁波ですね。参考文献[3]では、電磁波の反射に関してTorrance Sparrow則の方が実験値と合うと主張しています。
Torrance Sparrow則は1967年に発表されたもので、コンピュータグラフィックスのために考案されたものではないようです。図18に原文の一部を示します。“This paper is based on work done at the Heat Transfer Laboratory”とありますね。このことからも分かるように、Torrance氏とSparrow氏は伝熱の仕事でこの論文を書いたようです。というわけで、この論文により、電磁波の反射がランバート則には従わないことが実験で証明されました。筆者としてはこの点に加えて、高温物体からのふく射についても「本当にランバート則が妥当なのか?」と、少し疑問を抱いています。
Torrance Sparrow則を使ったコンピュータグラフィックスでリアルに表現できるのはお月さまだけのようです。
無限等比級数の和について
ここでは、筆者が昔、物理の先生に教えてもらった「なんちゃってマクローリン展開」を紹介します。無限等比級数の和の公式は次式でした(式51)。
等比級数の和の公式は2〜3行の簡単な計算で導出でき、無限等比級数の和もn→∞で求まります。また、式51の右辺をマクローリン展開することでも、同じ結果を導くことができますね。マクローリン展開は次の式で表されます(式52)。
なんちゃってマクローリン展開はというと、図19のように、単にa1を1−rで割算するのです。
展開式をド忘れしたときに使えますね。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング




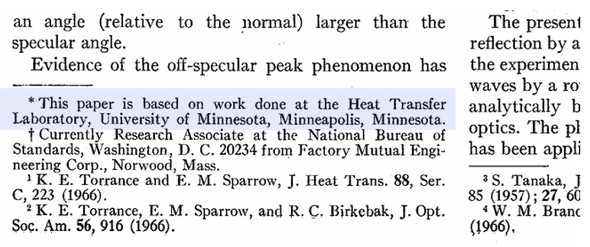
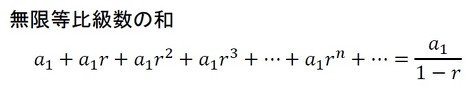 式51
式51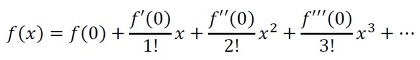 式52
式52