「ふく射」による熱の伝わり:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(7)(5/9 ページ)
真空蒸着装置の熱計算
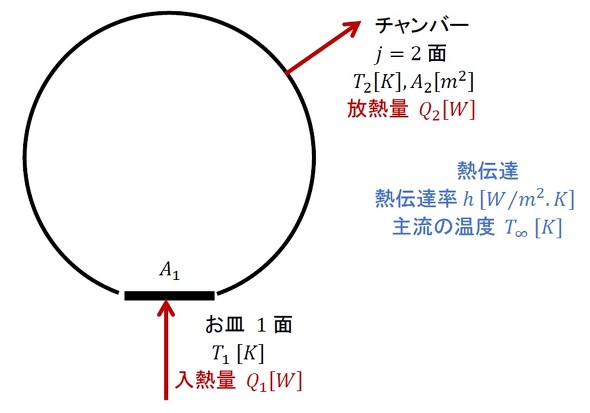
前述した計算法を真空蒸着装置に適用します。ただし、ここでは問題を簡単にすることとします。簡素化したモデルを図10に示します。
i面を1面、j面を2面と表記します。1面について、式36は次式となります(式37)。
2面については、1と2を入れ替えて次式となります(式38)。
T1とT2が決められていて、1面と2面との間の熱のやりとりを求める場合には、式37と式38の連立方程式を解き、J1、J2を求めて、式35から熱の移動量を導き出します。しかし今回の場合、T1は加熱したい温度であり既知ですが、T2は部屋の空気の温度T∞とチャンバー外側表面の熱伝達率hで決まるため未知数となります。つまり、未知数はJ1、J2、T2の3つになります。もう1つ式を作ります。図10のQ2は、熱伝達で部屋の空気に移動すると考えて次式で表せます(式39)。
式35から、Q1は次式となります(式40)。
1と2を入れ替えて、Q2は次式となります(式41)。
ここでは、式39と式41が等しいとしましょう。
これで、式37、式38、式42の連立方程式ができました。ですが、かなり困りものです……。ふく射の問題は、温度の4乗の項が出てきて4次方程式となります。4次方程式の解を陽の形で表すことができるとのことですが、この方法は止めておきましょう。
あらためて、以下に示す3つの式を作ります(式43〜45)。
そして、式46が最小になるように未知数を「Excel」のソルバー機能で求めます。
形態係数は1面(お皿)が放射する熱の全量が2面(チャンバー)に届くと考えて、次式とします(式47)。
式27を使うと、F21は以下となります。
しかし、少し変ですね……。図10を見てみると、2面からの放射のほとんどは2面に届きますが、今回のモデルはこの点を考慮していません。よって、近似計算となります。面の数を増やすと厳密な計算となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

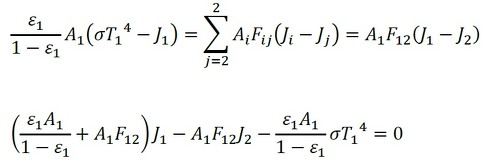 式37
式37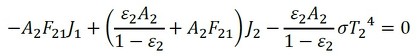 式38
式38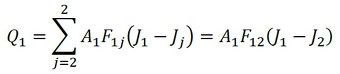 式40
式40 式42
式42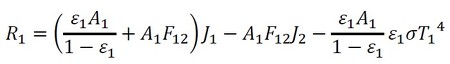 式43
式43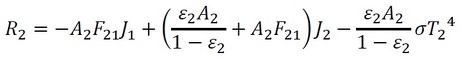 式44
式44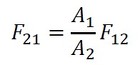 式48
式48





