「ふく射」による熱の伝わり:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(7)(8/9 ページ)
式34の考察
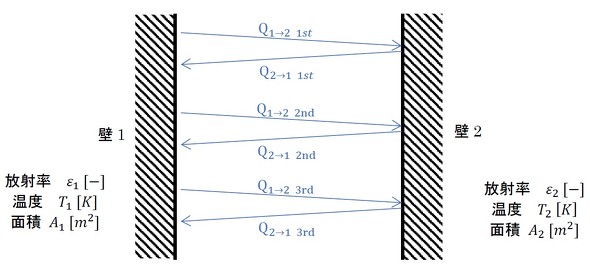
もう少しだけお付き合いください。天下り的に示した式34を確かめてみましょう。図20に示すような2つの壁を考えます。
もともと壁1にあった熱の放射と反射を考えます。
壁1が全空間に放射する熱量は以下の式です。
Q1=ε1σT14A1
そのうち、壁2に到達する熱量は以下の式です。
Q1→2 1st=Q1F12=ε1σT14A1F12
上記の熱が壁2で全空間に反射する熱量は以下の式です。
(1−ε2)ε1σT14A1F12
上記の熱が壁1に到達する熱量は以下の式です。
Q2→1 1st=(1−ε2)ε1σT14A1F12F21
上記の熱が壁1で全空間に反射する熱量は以下の式です。
(1−ε1)(1−ε2)ε1σT14A1F12F21
上記の熱が壁2に到達する熱量は以下の式です。
Q1→2 2nd=(1−ε1)(1−ε2)ε1σT14A1F12F21F12
上記の熱が壁2で全空間に反射する熱量は以下の式です。
(1−ε2)(1−ε1)(1−ε2)ε1σT14A1F12F21F12
上記の熱が壁1に到達する熱量は以下の式です。
Q2→1 2nd=(1−ε2)(1−ε1)(1−ε2)ε1σT14A1F12F21F12F21
上記の熱が壁1で全空間に反射する熱量は以下の式です。
(1−ε1)(1−ε2)(1−ε1)(1−ε2)ε1σT14A1F12F21F12F21
上記の熱が壁2に到達する熱量は以下の式です。
Q2→1 3rd=(1−ε1)(1−ε2)(1−ε1)(1−ε2)ε1σT14A1F12F21F12F21F12
もともと壁1にあった熱が壁2に到達する熱量の総和は次式となります(式53)。
初項がε1σT14A1F12、項比が(1−ε1)(1−ε2)F21F12の等比級数です。式54となります。
もともと壁1にあった熱なのですが、壁2での反射によって壁1に到達する熱量は次式となります(式55)。
これも等比級数なので次式となります。
次は、もともと壁2にあった熱の放射と反射を考えます。図21を使います。
壁2が全空間に放射する熱量は以下の式です。
Q2=ε2σT24A2
そのうち、壁1に到達する熱量は以下の式です。
Q2→1 1st=Q2F21=ε2σT24A2F21
上記の熱が壁1で全空間に反射する熱量は以下の式です。
(1−ε1)ε2σT24A2F21
上記の熱が壁2に到達する熱量は以下の式です。
Q1→2 1st=(1−ε1)ε2σT24A2F21F12
上記の熱が壁2で全空間に反射する熱量は以下の式です。
(1−ε2)(1−ε1)ε2σT24A2F21F12
上記の熱が壁1に到達する熱量は以下の式です。
Q2→1 2nd=(1−ε2)(1−ε1)ε2σT24A2F21F12F21
上記の熱が壁1で全空間に反射する熱量は以下の式です。
(1−ε1)(1−ε2)(1−ε1)ε2σT24A2F21F12F21
上記の熱が壁2に到達する熱量は以下の式です。
Q1→2 2nd=(1−ε1)(1−ε2)(1−ε1)ε2σT24A2F21F12F21F12
上記の熱が壁2で全空間に反射する熱量は以下の式です。
(1−ε2)(1−ε1)(1−ε2)(1−ε1)ε2σT24A2F21F12F21F12
上記の熱が壁1に到達する熱量は以下の式です。
Q2→1 3rd=(1−ε2)(1−ε1)(1−ε2)(1−ε1)ε2σT24A2F21F12F21F12F21
もともと壁2にあった熱が壁1に到達する熱量の総和は次式となります(式57)。
もともと壁2にあった熱が壁1での反射によって壁2に到達する熱量は次式となります(式58)。
壁1から壁2への熱の移動量は、壁1から壁2に到達する熱量から壁2から壁1に到達する熱量を差し引いたものなので次式となります(式59)。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

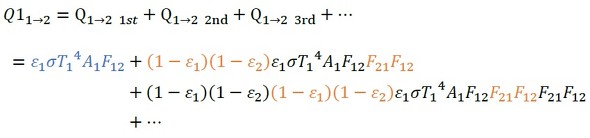 式53
式53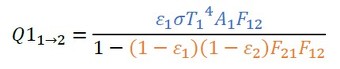 式54
式54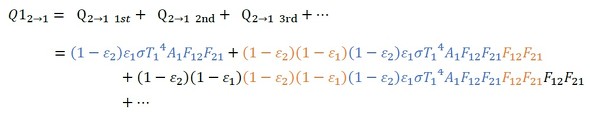
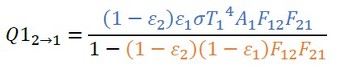 式56
式56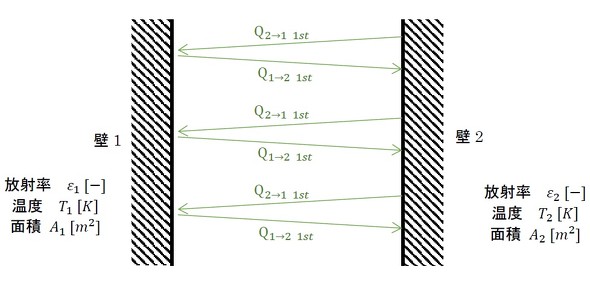
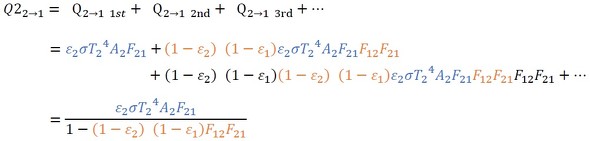

 式59
式59





