「ふく射」による熱の伝わり:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(7)(4/9 ページ)
蒸着装置
「ある部品に金属の薄い膜を貼り付ける」――。そんなニーズはさまざまな分野で見られます。このとき、真空中で金属を蒸発させて膜を形成する方法が用いられます。これを「真空蒸着」といいます。
筆者も学生時代、透過型電子顕微鏡の試料を作る際に、この蒸着装置を使った経験があります。
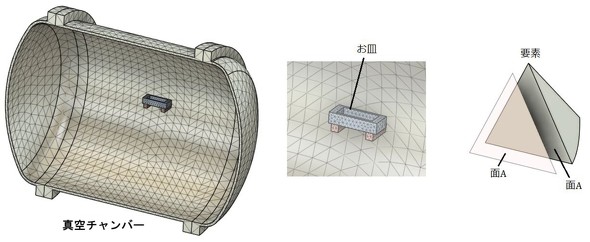
では、蒸着装置に使われるヒーターの設計をしましょう。図7に蒸着装置の一例を示します。「お皿」に蒸着したい金属を載せて、ヒーター(図では省略)で加熱します。金属を蒸発させるにはかなりの高温が必要になるため、ヒーターの容量も大きくなります。
お皿を加熱する温度は、場合によっては2000[degC]を超えることもあります。「支え」はお皿を固定するためのものです。今回はお皿を2000[degC]まで加熱するために必要なヒーターのワット数と、チャンバーの温度を求める問題に取り組みます。
図8に、シミュレーションモデルの例を示します。チャンバーの中身が見えるように2分の1モデルとしましたが、ふく射シミュレーションでは対称性があるとしても2分の1モデルは使えません。チャンバーは省略せずに全て要素分割されているとお考えください。
図8右図に1つの要素を示します。ふく射のシミュレーションでは、要素の空間を向いている面だけを使ったシェル要素のような要素(表皮要素)を使います。図のピンク色の要素です。
全ての表皮要素間の熱のやりとりを計算します。この手法を「ラジオシティ法」と呼びます。かなり計算量の多い方法ですので、今回はシミュレーションの紹介だけとなります。
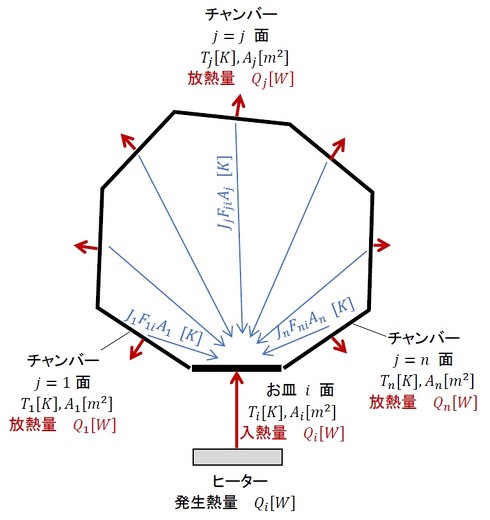
紙と鉛筆による方法を説明します。解析モデルを図9に示します。i面はお皿です。お皿の表面積がAiとなります。ヒーターによってQi[W]の熱がお皿に伝わります。1、2、……、j、……、n面は分割されたチャンバーの面です。チャンバーの面は熱伝達によって部屋の空気に伝わります。この量をQj[W]とします。
i面(お皿)がチャンバーに放射する熱流束を考えます。式29が考えられます。
式29の第1項は、ステファン・ボルツマンの法則によってi面が放射する熱です。第2項のρは反射率で、式5を使いました。そして、Giはというと、チャンバー(j面)からやってくる放射熱です。これをρ倍したものが反射されます。
Jiは放射する熱流束だと記しましたが、正確には「射度(Radiosity)」といって、i面からの見掛け上の放射熱流束です。Giはどんな量かというと、式30で表されます。
式の中に、また射度Jが登場しました。少し分かりづらいですね。しかし、こうしないと図4のような反射を繰り返す計算をする羽目になるようです。ヒーターの熱がi面を通じてチャンバー内に放射される熱Qiは、(出ていく熱−照らされた熱)であり、式31となります。出ていく熱の中に反射した熱が入っているため、引き算するのは「吸収した熱」ではなく「照らされた熱」となります。
式31右辺の第1項は出ていく熱、第2項は放射で照らされた熱で、その差がi面に供給される熱です。式29を変形します。
式32を式31に代入します(式33)。
もう1つ式を作ります。i面とj面間の放射熱流束qijを考えます。黒体放射の式(式28)をそのまま使います。式34となります。少し天下り的ですね。この式が本当に成立するかどうかを確認した結果を巻末に掲載しています。
Qiは次式で表すこともできます。次式を使うということは、図9において、赤色矢印は全て内側に向けなければなりません。しかし、分かりやすくj面側の矢印を外向きに描きました。そのため、式35のj面の計算結果はマイナス値となります。
式33と式35は等しいので、次式が成立します(式36)。
i面とj=1、2、……、j、……、n面で式36を作ることができます。式の数はn+1式です。未知数はJi、J1、J2、……、Jnとn+1個で、式の数と未知数が一致し、連立方程式が出来上がりました。これを解けば未知数が求まり、式35に代入すると各面を通過する熱量が求まります。各面の温度が既知の場合は行列計算で解くことが可能です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査


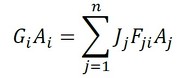 式30
式30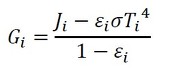 式32
式32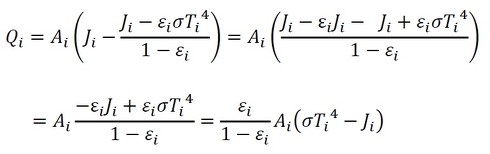 式33
式33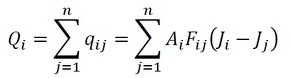 式35
式35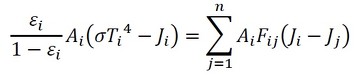 式36
式36





