第36回 コンピュータの並列処理とバス幅の増大:前田真一の最新実装技術あれこれ塾(3/3 ページ)
3.スーパーコンピュータ
このコプロセッサのたくさんの単純な計算を複数の小さなコンピュータで並列処理させる考えは、シミュレータなどの科学計算にも有効だとの考えが生まれました。
シミュレーションといっても実に多様ですが、実は多くのシミュレーションは膨大な数の単純な演算から成り立っています。
いま、単純な2次元の例で考えてみます。多くのシミュレーションでは解析する対象をセルと呼ばれる小さな領域に分けて解析します(図10)。
このセルの形状はいろいろなものがあり、大きさも均一に分けたり、境界部を外形に合わせたり、変化の大きいところを細かく分けたりといろいろです。
ここでは最も単純な正方形にします。
セルAにはセルa、b、c、dの4つのセルが接しています(図11)。
セルAとセルaの持つエネルギー(電圧や電界、磁界、温度などシミュレータによって異なります)の差によってある伝達関数FaでAとaの間でエネルギーが移動します。同じようにAとbの間の伝達関数はFb、AとcはFc、AとdはFdとなります(図12)。
この伝達関数はシミュレータによっていろいろありますが、関数自体はそれほど複雑なものではありません。
いまA、a、b、c、dの持つエネルギーをEA(t)、Ea(t)、Eb(t)、Ec(t)、Ed(t)とすると次のタイミングではAの持つエネルギー、EA(t+1)は、
EA(t+1)=E(At)+Fa(E(At)−E(at))+
Fb(EA(t)−Eb(t))+Fc(EA(t)−Ec(t))
+Fd(EA(t)−Ed(t))
となります(図13)。
伝達関数を使ったこの演算自体はそれほど複雑なものではありません。しかし、その演算数は膨大なものとなります。セルaはA以外にも3つのセルに接しています。セルb、c、dも同様に他のセルと接しています。
全てのセルに対してこの単純な演算を実行した結果、次のタイミングでの各セルの状態が分かり、それが次のタイミングでの計算のデータになります。これが3次元になればセルの総数もお互いに接するセルの数も増えます。セルの形状が複雑になれば、また、セルの総数もお互いに接するセルの数も増えます。
このような比較的簡単な演算を、膨大な数で行うには、多くのコプロセッサで並列処理をさせるのが効率的です。
このため科学計算用のアクセラレータが製品化されました。例えば、インテル社のXeonPhiコプロセッサでは幾つかの製品がありますが、60個程度のコプロセッサと、6〜16GBのメモリからなっています(図14)。
コプロセッサは4つの演算が並列処理できます。これがPCI-Expressボードに組み込まれ、1つのシステムで、複数枚を実装することができます。このような、メモリバスの並列化を見越して、新しいメモリ規格であるWide I/O規格では512bitのバス幅、規格策定中のHBM規格では1024bitのバス幅を規格としています。
もちろん今後、全てのコンピュータが多数のコプロセッサを持ち、大きな並列バスをもつとは限りません。
今後、ますます増大するネットワークをコントロールするためのネットワークサーバ、膨大なビッグデータを処理するためのコンピュータなど、求められる機能は同じではありません。
今後は、単純にコンピュータとか、スーパーコンピュータというだけでなく、目的とするアプリケーションに最適化されたコンピュータが求められてくるでしょう。
参考資料
- 1 「パソコン・グラフィックス入門」(1983年、オーム社):大原茂之、倉田了一(前田真一)、長谷川正治、加藤直之 共著
筆者紹介
前田 真一(マエダ シンイチ)
KEI Systems、日本サーキット。日米で、高速システムの開発/解析コンサルティングを手掛ける。
近著:「現場の即戦力シリーズ 見てわかる高速回路のノイズ解析」(技術評論社)
関連記事
- ≫前田真一の最新実装技術あれこれ塾
 SCE、PS4向けバーチャルリアリティーシステム「Project Morpheus」を試作
SCE、PS4向けバーチャルリアリティーシステム「Project Morpheus」を試作
ソニー・コンピュータエンタテインメントは、家庭用据え置き型ゲーム機「PlayStation 4」向けのバーチャルリアリティーシステム「Project Morpheus(プロジェクト モーフィアス)」を試作開発したと発表した。バイザースタイルのヘッドマウントユニットを頭部に装着することで、臨場感のある3D仮想空間を体験できる。 テレビとスマホで黒字化したソニー、反撃ののろしは上がったのか
テレビとスマホで黒字化したソニー、反撃ののろしは上がったのか
ソニーが発表した2014年3月期第1四半期決算では、スマートフォン事業とテレビ事業が大幅に損益改善した他、為替の好影響を受け、最終損益の黒字化を達成した。 CPU・MPUはどうやって動く?
CPU・MPUはどうやって動く?
CPU(MPU)の基礎知識をおさらいする。重要なのは「どこから命令を持ってくるか」と「どこに実行結果を書き込むか」の2点だ ソニー、復活へ道半ば――鍵を握る“感性価値”商品
ソニー、復活へ道半ば――鍵を握る“感性価値”商品
ソニーは2015年3月期に売上高8兆5000億円、営業利益率5%以上、ROE10%の中期目標を発表した。しかし、中核と位置付けるエレクトロニクス主力3事業では積極投資を進めるものの、前回発表した目標数値を下方修正し、復活への道が容易ではないことをうかがわせた。
Copyright © ITmedia, Inc. All Rights Reserved.
Factory Automationの記事ランキング
- これ板金? ちょっと何言っているかよく…第38回優秀板金製品技能フェア各賞紹介
- AGVか、それともAMRか……無人搬送機導入時の注意点
- 「そのラダープログラム10年後も読めますか」――オムロンが描くAI活用
- 同じ原理は超高速で走る“あれ”にも! ある装置の音
- DMG森精機と東大がMXセンターを設立、森氏は“機上計測”に関心
- 「深夜特急」のイラン
- 最高速度5m/sの自由な経路を構築、THKが搬送システム向けガイド受注開始
- 工場データ収集の9割で通信トラブル経験、製造業の現場担当者約1000人調査
- 多種多様なセンサーを統合し、仮想計測も可能なプラットフォームを発表
- 最大4mの長距離検出と、黒色や光沢ワークなども高精度測定を両立
コーナーリンク
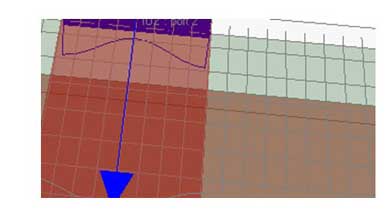 図10:多くのシミュレータはセルを使う
図10:多くのシミュレータはセルを使う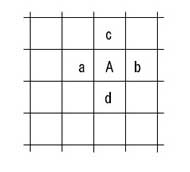 図11:2次元の簡単なモデル
図11:2次元の簡単なモデル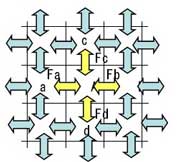 図12:セル間のエネルギー伝達関数
図12:セル間のエネルギー伝達関数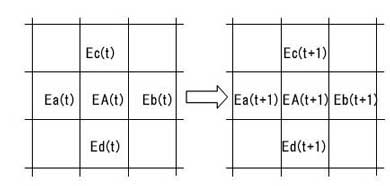 図13:cellのエネルギー変化
図13:cellのエネルギー変化 図14:Xeon Phi(from Intel)
図14:Xeon Phi(from Intel)




