第31回 損失:前田真一の最新実装技術あれこれ塾(4/4 ページ)
4.抵抗損失と基板表面粗さ
超伝導でない限り、銅をはじめとする導体にも、小さな値ですが、抵抗が存在します。
抵抗Rに電流Iを流すと、電気エネルギーWは熱エネルギーに変化します。
W=I2・R……(4)
基板の銅配線の抵抗Rは配線の断面積Sに反比例し、配線の長さlに比例します。
R=ρ・l/S……(5)
ここで、ρは体積伝導率と呼ばれる導体材料の定数で、100℃の銅ではρ=2.23e-8・Ωmとなります。
このため、大電流が流れる電源配線では、断面積Sを大きくするために、厚い銅箔を使い、配線幅を太くします。
一般の信号では電流は10〜20mA程度で、銅箔の幅が100μm、厚さは18μm程度です。これで長さ10cmの配線の抵抗は銅のρは25℃で1.72e-8・Ωmなので、0.955Ωとなります。
振幅1Vの信号が20mAの電流で伝播する場合、0.955Ωの配線での電圧降下はおよそ0.002Vとなり、出力の電圧は0.998Vになります(図12)。
この配線による損失Lrは
Lr=log(0.998/1)=-0.00087dB
となり、ほぼ無視できるほど小さな値です。
しかし、信号の周波数が高くなると電流は導体の表面にしか流れなくなります。これを表皮効果といい、導体の表面、電流が流れる深さを表皮深さと呼びます(図13)。
この表皮深さ(δ)は信号の周波数fの平方根に反比例します。
δ=√πfμκ……(6)
ここで、μとκはおのおの導体材料に依存する係数で、銅の場合は
μ=4πe-7
κ=1/(2e-8)
です。
これらの値を使うと、表皮深さは
δ=8.5μm(70MHz)
δ=2.25μm(1GHz)
δ=1μm(5GHz)
程度になります。
基板配線の銅箔厚さは17μm程度なので、信号速度が70MHz以下では銅箔全体に信号が流れ、表皮効果の影響はありません(図14)。実際は100MHz程度でも表皮効果の影響は非常に小さいので無視できます。
しかし、数百MHz以上の信号では表皮効果の影響は無視できません。
ここで、1GHzの場合を検証してみましょう。
一般に基板配線の銅箔はコア材に接している面は銅箔とコアの接着を強くし、銅箔が簡単に剥がれないように銅箔の表面を荒くして機械的な接着強度を増やす加工がされています(図15)。
このように表面を荒くして楔のように基板材料に食い込みせっやく力を高める効果をアンカー(錨:いかり)効果と呼びます。
しかし、このように荒い表面には表皮厚さが薄い場合には電流が流れません。
幅100μm、高さ17μmで断面積が理想的な方形とした場合(図16)、配線に1GHzの信号が流れる断面積Sは
S=100e-6×2.25e-6
+((17e-6-2.25e-6)×2.25e-6)×2
=291.375e-12(m2)
となります。
この断面積で25℃、10cmの配線が持つ抵抗値は
2.23e-8×0.1/291.375e-12
=7.65Ω
となります。
1V、20mAの信号電流が流れると配線による電圧降下は0.153mVで配線による損失Lrは
Lr=log(0.847/1)=-0.072dB
となります。
5GHzでは抵抗値は17Ωで損失は-0.66dBとなります。
ここでは、銅箔は基板コア材との接触面以外は理想的な平滑面としましたが、実際の銅箔では数μmの凹凸があります。この銅箔の表面粗さの効果を考慮する必要があります。
参考文献
- 2.5D Interposers; Organics vs. Silicon vs. Glass:by Prof. Rao R. Tummala, Chip Scale Review July-August, 2013
- 1999 Packaging Databook:Intel Corporation
筆者紹介
前田 真一(マエダ シンイチ)
KEI Systems、日本サーキット。日米で、高速システムの開発/解析コンサルティングを手掛ける。
近著:「現場の即戦力シリーズ 見てわかる高速回路のノイズ解析」(技術評論社)
関連記事
- ≫前田真一の最新実装技術あれこれ塾
 摩擦があると、どうしてエネルギーを失うのか
摩擦があると、どうしてエネルギーを失うのか
摩擦によって力学的エネルギーが損失することを理解するためには、まずニュートンの運動方程式をきちんと理解する必要がある。 SiC-MOSFETの課題克服へ、新材料を用いたゲート絶縁膜で信頼性を向上
SiC-MOSFETの課題克服へ、新材料を用いたゲート絶縁膜で信頼性を向上
SiC-MOSFETの量産採用に向けた課題の1つとして挙げられているのが、酸化シリコンを用いたゲート絶縁膜に起因する動作時の信頼性の低さだ。大阪大学と京都大学、ローム、東京エレクトロンは、AlON(アルミニウム酸窒化物)を用いたゲート絶縁膜によって、SiC-MOSFETの信頼性を高める技術を開発した。
Copyright © ITmedia, Inc. All Rights Reserved.
Factory Automationの記事ランキング
- これ板金? ちょっと何言っているかよく…第38回優秀板金製品技能フェア各賞紹介
- 「そのラダープログラム10年後も読めますか」――オムロンが描くAI活用
- 同じ原理は超高速で走る“あれ”にも! ある装置の音
- DMG森精機と東大がMXセンターを設立、森氏は“機上計測”に関心
- 「深夜特急」のイラン
- 物流自動化は「入れて終わり」ではない、本社と現場の分断を越える“キーマン”とは
- ロックウェル「自律型工場」への道筋、5つのステップと7つの技術要素
- 2033年に年間1万人相当の供給体制、第1弾は手足のシンクロ可能な移動ロボ
- 鋳造/鍛造品向け切削加工AIの共同開発合意、アルムと神戸製鋼所
- AGVか、それともAMRか……無人搬送機導入時の注意点
コーナーリンク
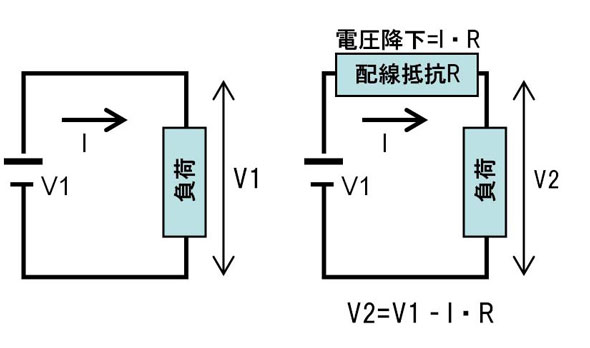 図12:配線の持つ抵抗分の影響
図12:配線の持つ抵抗分の影響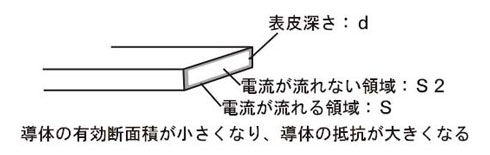 図13:表皮深さと導体の抵抗値
図13:表皮深さと導体の抵抗値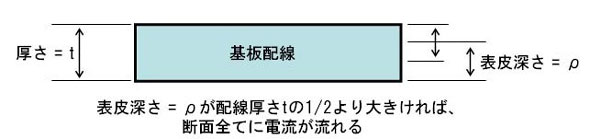 図14:遅い信号では表皮効果の影響はない
図14:遅い信号では表皮効果の影響はない 図15:アンカー効果
図15:アンカー効果 図16:表皮深さが小さい場合
図16:表皮深さが小さい場合




