幾何公差の相互関係は、F<O<L:製図を極める! 幾何公差徹底攻略(10)(2/2 ページ)
幾何公差同士の相互関係
例えば、ある面に直角度を指示した場合を考えてみましょう(図5)。
このデータムAに対して直角度が指示された面には、平面度が指示されていません。それでは、独立の原則のように直角度と平面度を別々にして考えてもいいかというと、そうではないのです。
この直角度の示す範囲を図示してみます。図6のように直角度0.05を守るには、平面度も0.05以下でないと直角度の領域からはみ出してしまいます。
次に、ある面に対し、輪郭度公差を指示した場合を考えてみましょう(図7)。
この面の輪郭度が指示された面には、データムAに対する平行度や平面度が指示されていません。面の輪郭度の示す範囲を図示してみます(図8)。
図8のように、上面の高さ位置を表す面の輪郭度0.05を守るには、データムAに対する平行度と平面度のどちらも0.05以下でないと面の輪郭度の領域からはみ出してしまいます。
以上のことから、幾何公差には下記の相互関係があることが分かります。
形状公差 < 姿勢公差 < 位置公差
Form < Orientation < Location
つまり、姿勢公差を指示するということは関連する形状公差を含み、位置公差を指示するということは関連する姿勢公差と形状公差を含むのです。
上記の関係を暗記しやすくするため、それぞれの英語の頭文字を利用して、F<O<Lの相互関係と覚えておきましょう。
従って、機能上必要がある場合には、下記のようにそれぞれの幾何特性を細かく指示することも可能です。
特に理由がない限り、図9のように姿勢公差や形状公差まで細かく指示する必要性はなく、図7のように、面の輪郭度を満足させれば、自動的に平行度や平面度は小さくなると考えます。
このように幾何公差はロジカルに展開できることを知っていただければと思います。
全10回にわたった「製図を極める! 幾何公差徹底攻略」は、これにて終了です。「カタチが崩れる」といい出したら、ありとあらゆる面が崩れることになってしまいます。そう考えると全ての部分に幾何公差が必要になってしまい、逆に幾何公差が使えなくなってしまいます。
まずは、寸法公差でどうしても制御できないカタチの崩れから、幾何公差を使ってみてはいかがでしょうか。
幾何公差は、いい出したらきりがないほどへ理屈をいうことが可能です。
幾何公差を使いこなすポイントは、頭の中で「へ理屈」を考えつつ、それを口に出さないことです!
ある程度常識の範囲内で加工によるカタチの崩れを予測し、“いかに単純に幾何公差を指示するか”に尽きると思います。
読者の皆さんが、正しい幾何公差の作法を身に付け、グローバル対応できる図面が描けることを願って、あいさつに代えさせていただきます。(See You!)
◎併せて読みたい「CAD」関連ホワイトペーパー:
» 主要7製品を完全網羅! 製品選定・比較に役立つ「商用3D CADカタログ 完全版」
» 【導入事例】食品加工機械メーカー不二精機による“3D CAD推進”
関連記事
 最近のJISだと「寸法公差」ではなく「サイズ公差」なのはなぜか
最近のJISだと「寸法公差」ではなく「サイズ公差」なのはなぜか
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回はJIS製図における「サイズ」「サイズ公差」「幾何公差」について考える。 「設計から製図までチャレンジしてみよう」の巻
「設計から製図までチャレンジしてみよう」の巻
図面にも触れたことのないような初心者を対象とした、図面の読み方・描き方講座。お題をクリアしながら、解説を読み進めていくことで、いつしか図面の読み描きができるようになる! 今回は、集大成として設計から製図までの一連の作業に挑戦する。 2Dと3Dの融合と、公差設計の重要性
2Dと3Dの融合と、公差設計の重要性
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は構想設計から詳細設計までのプロセスを振り返りながら、公差設計の重要性について考える。 設計者必携! 板金設計がマスターできる絵辞書
設計者必携! 板金設計がマスターできる絵辞書
これまでの「甚さんシリーズ」の解説を少し振り返った後、この連載で使うツール「板金設計の50%がマスターできる絵辞書」を紹介する。 いまさら聞けない!? 製図の素朴な疑問たち
いまさら聞けない!? 製図の素朴な疑問たち
「外形線と寸法補助線は接して描かなければならないのか」「φは『パイ』と読むのか」などいまさら聞けない素朴な質問ばかりを集めてみた。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
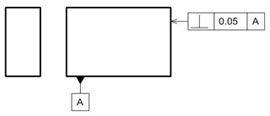 図5 直角度が指示された面
図5 直角度が指示された面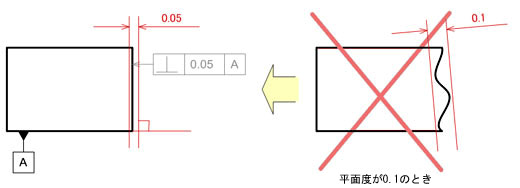 図6 直角度の意味する領域
図6 直角度の意味する領域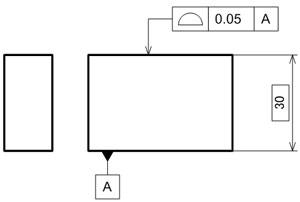 図7 位置公差として面の輪郭度が指示された面
図7 位置公差として面の輪郭度が指示された面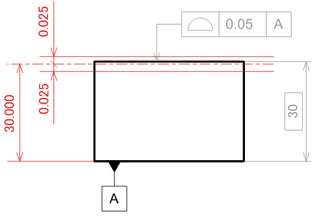 図8 面の輪郭度の意味する領域
図8 面の輪郭度の意味する領域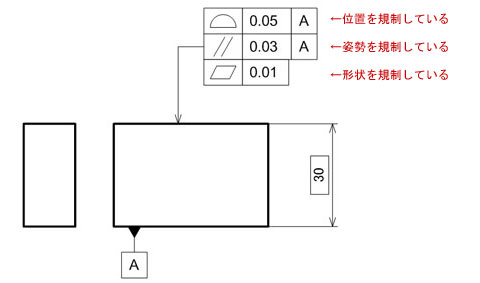 図9 幾何特性を分けて指示した場合
図9 幾何特性を分けて指示した場合






