同軸かどうか寸法で表せないときは、神頼み!?:製図を極める! 幾何公差徹底攻略(8)(1/2 ページ)
外径に対して内径の同軸ずれが発生するかもしれないことに気が付いたら? 寸法線ではどうしても表現できないし……
前回までに形状公差はその絶対的なカタチの崩れを規制し、姿勢公差はデータムに対する角度ずれを規制することを学習しました。今回は4つのグループに分類される幾何特性のうち3番目の位置ずれを制御する位置公差です。
位置公差とは
位置公差とは、対象となる形体がデータムに関連して、中心点や軸線、中心平面などが、幾何学的に正しい位置(Location)に対して偏差の許容値内にあるかを規定するものです。幾何公差の分類の中でデータムを参照することから「関連形体」と呼ばれます。
位置公差に分類される幾何特性で、同軸度はデータム軸と同一線上(つまり同軸)からの位置ずれを規定し、対称度は対称形状の部品におけるデータム平面と同一平面上から位置ずれを規定します。また位置度は基準と設定した面から理論寸法で示された位置のずれを規定します。つまり位置公差は、寸法では表現不可能なゼロゼロの関係となる位置を表現できることが最大の特徴です! また、寸法を2点間の距離で測定するのではなく、測定治具を基準として位置を規定したりします。
位置公差には、次の5つの幾何公差があります。
- 同軸度(Coaxiality)/同心度(Concentricity)
- 対称度(Symmetry)
- 位置度(Position)
- 線の輪郭度(Profile of a line)
- 面の輪郭度(Profile of a surface)
このように5種類もある位置公差は次のように分類できます。
位置度公差の中でも、比較的図面に見ることができるものに同軸度があります。しかしそれ以外の対称度や位置度を見かけることはほとんどないといっても過言ではありません。
同軸度と同心度の意味の違いを知らない人が多く存在します。ある程度長さのある軸部品に対して「同軸度」という言葉を使い、平ワッシャのような円盤状の部品に対して「同心度」という言葉を使います。同軸と同心の呼び方が切り替わる長さは明示されておらず、図面上で指示される記号は同じものなので、感覚的に呼び分けても問題はないでしょう。
位置度は、形状に崩れさえなければ寸法公差でほぼ代用が可能といえます。日本の製造業のスキルの高さから、四角いブロックに穴を開ける場合において、外形寸法に公差がなくてもブロックの6面は、それぞれ平らな面に仕上げられ、隣り合う面は直角に、対向する面は平行に加工されてきたため、寸法公差でばらつきの範囲を示しても特に問題は発生しませんでした。
ところが同軸度や対称度は、寸法線すら記入されないために、設計者は何も指示をしません。それが当たり前のように図面を描いてきたのです。そのような認識で問題が起こらなかったのは、加工者がその部品の構造を推理し寸法公差から判断して、崩れのない高精度な部品を納入してくれたおかげ。「中心からずれて、後で文句いわれても困る」と感じるからです。
例えば、下記に示すような円柱の同軸上に穴が開いたパイプ形状の部品図を描くとします。設計者が100人いたら99人は図2のような図面を描き出図すると思います。
ここで、外径に対して内径の同軸ずれが発生するかもしれないことに気が付いたとしましょう。寸法線ではどうしても表現できません。
そう、神様にお願いをするしかないのです!
しかし日ごろの行いを考えると、神様が必ずしも願いをかなえてくれるとは限りません。そこで、次なる手段である「外径と内径は同軸のこと」という注記を図面に描くことを思い付き、安心してしまうものです。
ただこの注記では、「同軸からのずれを許さない」という意味になってしまうのです。加工者は同軸になるように気を付けて加工してくれますが、そのずれ量を厳密なゼロにできません。そのため、検査で良品・不良品の判断ができない図面となってしまいます。
同様に、丸軸の中央に穴を貫通させる部品を設計したとします(図3)。
この部品も穴を円筒軸の中央、つまり左右対称位置に開けて欲しいという意図が寸法線で表現する手段がありません。円弧の頂点に狂いなくドリルで掘り込むことは、大変難しい加工といえます。
同軸形状や対称形状は必ず設計形状に盛り込まれます。それなのに同軸であって欲しいこと、対称であって欲しいことを設計者が訴えなければ、図面に意思が入らないのです。これが幾何公差を使いこなすための大きなヒントとなります。
幾何公差は全部で14種類ありますが、寸法線でどうやっても表現できない同軸度と対称度は優先して使用すべき幾何公差といえます!
本記事では、位置公差のうち代表的な3つの特性の定義とともに、よく使われるだろう代表的な図面指示例を併せて確認していきます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
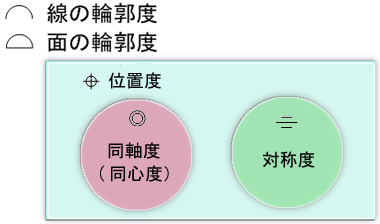 図1 位置公差の分類
図1 位置公差の分類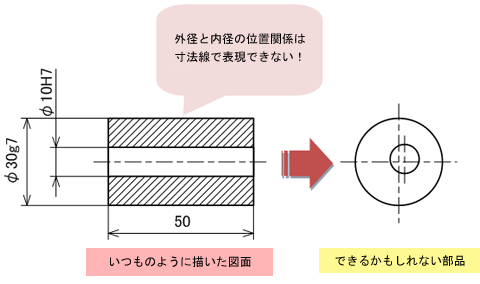 図2 同軸度を気にしなければいけない図面とは
図2 同軸度を気にしなければいけない図面とは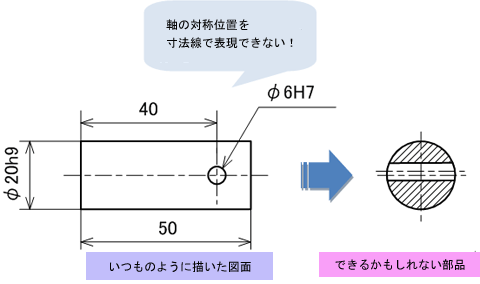 図3 対称度を気にしなければいけない図面とは
図3 対称度を気にしなければいけない図面とは





