理解しづらい傾斜度も、グループ分けでスッキリ:製図を極める! 幾何公差徹底攻略(7)(1/2 ページ)
平行度と直角度は分かるけど、傾斜度はよく分からないという人! ややこしく考え過ぎないで、シンプルに考えてみよう。
前回、幾何特性のうち基本となる形状公差を学習しました。「形状公差には、データムを付けてはいけない」ことが分かったと思います。
今回以降で解説する、残りの幾何特性グループ(姿勢公差、位置公差、振れ公差)は必ずデータムを参照します。データムを参照するということは、形体の一部を基準として利用し、対象となる形体の幾何特性を指示するものです。
姿勢公差とは
「姿勢公差」とは、対象となる形体がデータムに関連して、平行や直角、任意の角度を持つ幾何学的に正しい姿勢を表す偏差の許容値内にあるかを規定することです。幾何公差の分類の中でデータムを参照することから「関連形体」と呼ばれます。
姿勢公差に分類される幾何特性で、平行度は0度(あるいは180度)を規定し、直角度は90度(あるいは270度)を規定します。それ以外の任意の角度を規定するものが傾斜度です。つまり、姿勢公差は、データムに対する対象形体の角度特性を表すものなのです!
姿勢公差は、次の5つに分類できます。
- 平行度(Parallelism)
- 直角度(Perpendicularity)
- 傾斜度(Angularity)
- 線の輪郭度(Profile of a line)
- 面の輪郭度(Profile of a surface)
このように5種類もある姿勢公差は、さらに図1のように分類できます。
図1に線の輪郭度と面の輪郭度の関係を記載していますが、姿勢公差でこれらを使うことはまれなケースだと思われるため、今回は解説を省略します。
「傾斜度」は360度全周を網羅し、その中でも0度(180度)と90度(270度)のピンポイントで平行度と直角度を使うものだと理解できます。
筆者が開催するセミナーで幾何公差の認識度アンケートを取るとたいてい、平行度と直角度は認識度の上位に入りますし、実際、身近な図面でも多く見掛けます。ところが傾斜度となると、ほとんどの人が理解していないという結果になったことから、多くの人が苦手意識を持ちやすいことがうかがえます。でも上記のグループ分けに基づいて理解すれば、傾斜度が特別な幾何特性ではないことが分かることでしょう。
姿勢公差は角度を規制することから、幾何公差領域を角度バラツキの領域で単位は「度」と勘違いする人もいますが、幾何公差値の単位はあくまでも「mm」です。従って、平行度であれ、直角度であれ、傾斜度であれ、対象形体が穴の軸線の場合の公差領域は円筒内あるいは平行2平面間となることが一般的です(図2)。
本記事では、姿勢公差のうち、代表的な3つの特性の定義とともに、よく使われる代表的な図面指示例を併せて確認していきます。
平行度
JISによると、「平行度(Parallelism)とは、データム直線またはデータム平面に対して平行な幾何学的直線または幾何学的平面からの平行であるべき直線形体または平面形体の狂いの大きさをいう」と定義されます。
データムに対して平行であって欲しいという形体に対して指示するものです。
加工者の不注意がない限り、旋盤やフライス盤で加工された部品の面や穴の平行が大きく崩れることは、ほとんどありませんが、設計意図を表すために必要な場合はその旨を加工者に伝える必要があります。
図3に示す図面例は、ブロックの下面をデータムとし、最上面全体がデータム平面に平行である0.03mm離れた平行2平面間にあれば、合格品と判断されるものです。
下面と最上面に高さの寸法公差が記入されていますが、「独立の原則」に従うために高さバラツキ(±0.1mm)とは無関係に平行度を満足させればよいということです。
独立の原則:「図面上に個々に指示した寸法および幾何特性に対する要求事項は、それらの間に特別の関係が指定されない限り、独立に適用する。それゆえ何も関係が指定されていない場合には、幾何公差は形体の寸法に無関係に適用し、幾何公差と寸法公差は関係ないものとして扱う」(「JIS B 0024」より引用)
図4に示す図面例は、ブロックの下面をデータムとし、穴の中心線が、データムと平行な直径0.02mmの円柱の中にあれば合格品と判断されるものです。
下面と穴の中心線に高さの寸法公差が記入されていますが、独立の原則に従うために高さバラツキ(±0.1mm)とは無関係に平行度を満足させればよいということです。
どちらの例も、平行という姿勢だけを規制するものであって、幾何公差として位置までは規制しません。平行度の有用性として、今まで寸法公差で「90°±30’」(90度±30分)や「30°±1°」(30度±1度)と寸法公差指示はできても、唯一、平行形状の場合は「0°±30’」(0度±30分)のように寸法公差で指示することが製図ルール上では不可能だったため、直角度や傾斜度に比べると必然的に使う頻度が高い特性といえます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
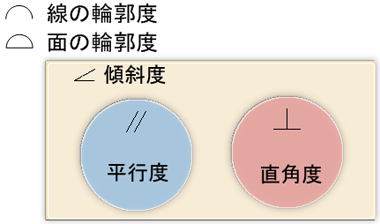 図1 姿勢公差の分類
図1 姿勢公差の分類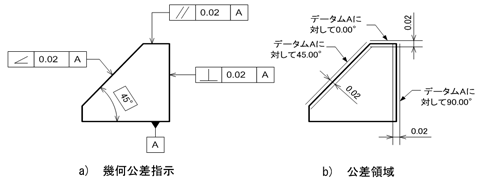 図2 姿勢公差の示す領域
図2 姿勢公差の示す領域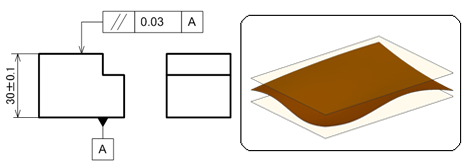 図3 平行度の指示例と領域(面指示の場合):右側の領域を示すイラストは、データムに対して平行な平行2平面を意味します
図3 平行度の指示例と領域(面指示の場合):右側の領域を示すイラストは、データムに対して平行な平行2平面を意味します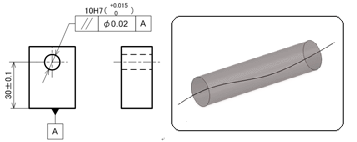 図4 平行度の指示例と領域(軸線指示の場合):右側の領域を示すイラストは、データムに対して平行な円筒を意味します
図4 平行度の指示例と領域(軸線指示の場合):右側の領域を示すイラストは、データムに対して平行な円筒を意味します





